|
|
Example: Noise Cancellation using the LMS Algorithm
Adaptive filters are required when it is necessary for a digital filter's characteristics to be variable,
adapting to changing signal characteristics. Such filters can be classed as 'self designing' in that they rely upon a recursive mathematical
algorithm, that allow them to perform satisfactorily in an environment where complete knowledge of the signal of interest (desired signal)
and noise is not known. As a consequence, adaptive filters, such as the LMS (least mean squared) algorithm have been used in many real world
applications such as biomedical signal enhancement, system identification and noise cancellation. The following example demonstrates the
enhancement of a 100Hz signal buried in band limited white noise, by virtue of a 30th order FIR LMS filter.
Adaptive line enhancement (ALE)
Adaptive line enhancement (ALE) refers to the case where a noisy
signal, x(n) consisting of a sinusoidal component, s(n) is available and the requirement is to remove the noise part of the
signal, n(n). This may be achieved by the arrangement shown below. It consists of a de-correlation stage, symbolized by
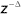 and an adaptive
predictor. The de-correlation stage attempts to remove any correlation that may exist between the samples of noise, by shifting them samples and an adaptive
predictor. The de-correlation stage attempts to remove any correlation that may exist between the samples of noise, by shifting them samples
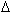 apart.
As a result, the predictor can only make a prediction about the sinusoidal component of u(n), and when adapted to minimize the instantaneous
squared error output, e(n), the line enhancer will be a filter optimized (the Wiener solution) or tuned to the sinusoidal component. apart.
As a result, the predictor can only make a prediction about the sinusoidal component of u(n), and when adapted to minimize the instantaneous
squared error output, e(n), the line enhancer will be a filter optimized (the Wiener solution) or tuned to the sinusoidal component.
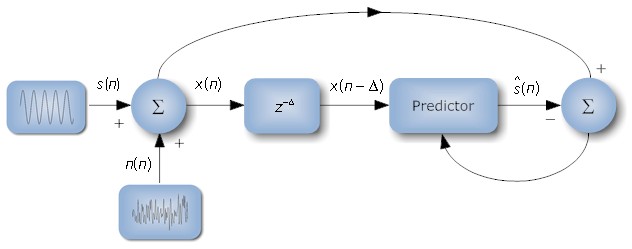
Analyzing the block diagram a little further, notice how the input to
the adaptive filter is actually
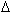 samples behind the primary input signal,
x(n), since the de-correlation stage has introduced a phase shift. Therefore, in order to time align the enhanced signal, ŝ(n)
with the input signal, x(n) the adaptive filter must be able to 'predict ahead' in time (formally referred as 'forward linear prediction'),
by optimizing its filter coefficients in a least squares sense, such that the instantaneous squared error is minimized. samples behind the primary input signal,
x(n), since the de-correlation stage has introduced a phase shift. Therefore, in order to time align the enhanced signal, ŝ(n)
with the input signal, x(n) the adaptive filter must be able to 'predict ahead' in time (formally referred as 'forward linear prediction'),
by optimizing its filter coefficients in a least squares sense, such that the instantaneous squared error is minimized.
|
 Flash video of the optimization. Flash video of the optimization.
|
 |
|
|