ASN Filter Designer DSP C# .NET SDK user’s guide

Overview

This document gives an overview to use the ASN Filter Designer’s C# SDK for .NET applications in Microsoft Visual studio.

The content is as follows:

• Folder structure generated project from filter designer
• Filter cascade and non-linear functions
• Filter definition class description

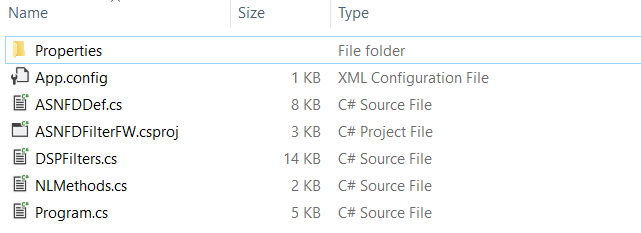
Folder structure generated project from filter designer

C# project folder form the Filter Designer software has following files and folders in it.

Properties, App.config – These files are required visual studio project dependencies.

ASNFDFilterFW.csproj – Microsoft Visual studio project files.

Program.cs – Contains example code to demonstrate the use of the SDK.

ASNFDDef.cs – This file has the primary filter class definition used for holding properties of the filter cascade that has been designed.

DSPFilters.cs – This file has all the libraries required for using the filter code.

NLMethods.cs – This file has a class for non-linear math functions required for the pre and post-processing of the signal.

Filter cascade and non-linear functions

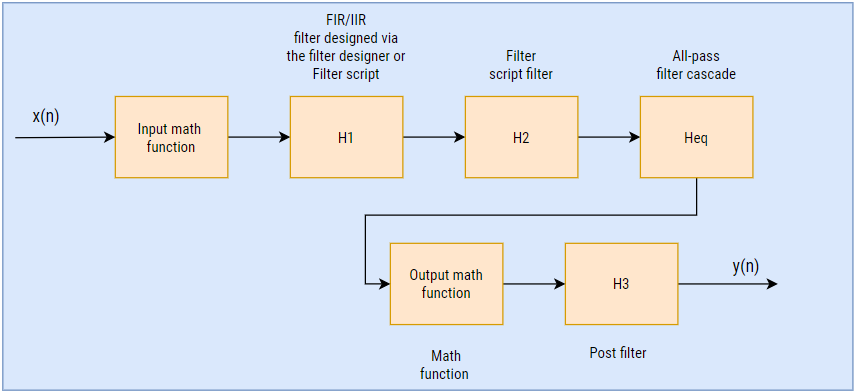
In order to implement a complete application, the ASN Filter Designer uses a combination of filters and non-linear functions, as described below in the architecture diagram. All blocks can be enabled or disabled from within the ASN Filter Designer depending on the user’s requirements.

Depending on the application, we can enable or disable Input and Output math functions. These functions are helpful for pre- or post-processing operations on the signal. The ASN Filter Designer supports the following math functions. You can select one of them according to your application’s needs.

Function ()	Math operation	Description
None	–	Disable the function block.
Abs	\(\displaystyle |x|=\sqrt{a^2+b^2}\)	Absolute.
Ln	\(\displaystyle log_e x\)	Natural logarithm.
Angle	\(\displaystyle \tan^{-1}(\frac{b}{a})\)	Compute the arctangent (phase in radians).
RMS	\(\displaystyle \frac{\sqrt{a^2+b^2}}{\sqrt{2}}\)	Root mean square.
Sqr	\(\displaystyle x^2\)	Square.
Sqrt	\(\displaystyle \sqrt{x}\)	Square root.
TKEO	\(\displaystyle y(n)=x^2 (n-1)-x(n)(x-2)\)	TKEO (Teager-Kaiser energy operator) algorithm.

The H1 (primary) filter(s) are designed via standard prototype methods, such as Butterworth, Chebyshev for IIR filters, and Parks-McClellan for FIR filters using the UI within the tool.

The H2 filter block implements a single section IIR/FIR floating point filter. This filter is available for performing experiments with the P-Z editor or the ASN FilterScript scripting language. The FilterScript language is primarily intended as a sandbox concept, allowing for the design and experimentation of transfer functions with symbolic mathematical expressions. Both H1 and H2 filters may be fully programmed using FilterScript.

Unlike the H1 and H2 filters, the H3 filter is always lowpass and is preceded by an optional mathematical function operation (i.e., Abs, Angle, Ln, RMS, Sqr or Sqrt, and TKEO).

The following four filters are supported:

Type	Transfer function	Gain at DC	Order
IIR	\(\displaystyle H_3 (z)= \frac{(1+2z^{-1}+z^{-2})}{(1+2αz^{-1}+α^2 z^{-2} )} \)	\(\displaystyle \frac{(1+2α+α^2)}{4} \)	2
Moving Average	\(\displaystyle H_3 (z)=1+z^{-1}+z^{-2}… +z^{-M}\)	\(\displaystyle \frac{1}{(M+1)}\)	1-200
Feed through	\(\displaystyle H_3 (z)=1\)	\(\displaystyle 1\)	–
Median	data window	–	3-195

Filter definition class description

The variables discussed below are from ASNFDDefinition class. The ASN Filter Designer sets all of these variables according to the designed filter cascade and quantisation selected. The library currently supports floating point Real and Complex filters only. The following keywords are used for describing each datatype: float (single precision), double (double precision), complex double (complex double precision).

The content is as follows:

1. Set coefficients of the H1 filter
2. Set coefficients of the H2 filter
3. Set coefficients of the Heq filter
4. Set coefficients of the H3 filter
5. Perform the data filtering operation
6. Specify inputs and output math functions
7. Initialise the filters
8. Reset the filter cascade

Set coefficients of the H1 filter

public float[] H1Numerator;
public float[] H1Denominator;
public float[,] H1SOS;
public int H1NumBiquads;

Description

These variables are used for specifying coefficients of the H1 filter.

Example

H1SOS = [,] {{0.15919464484408, 0.15919464484408, 0.00000000000000, 0.68165454497010, 0.00000000000000},{0.04362563518631, 0.01333388307825, 0.04362563518631, 1.38973983422963,-0.49030168693325}};
H1Numerator = [] {0.98453370859690, -0.98453370859690,0.98453370859690, -0.98453370859690};

H1Denominator = [] {-1.00000000000000, 0.96906741719379, -0.92300230934793, 0.89445146398370};

Set coefficients of the H2 filter

public float[] H2Numerator;
public float[] H2Denominator;

Description

These variables are used for specifying coefficients of the H2 filter.

Example

H2Numerator = [] {0.98453370859690, -0.98453370859690, 0.98453370859690, -0.98453370859690};

H2Denominator = [] {-1.00000000000000, 0.96906741719379, -0.92300230934793, 0.89445146398370};

Set coefficients of the Heq filter

public float[] HeqSOS;
public int HeqNumBiquads;

Description

These variables are used for specifying coefficients of the H2 filter.

Example

HeqNumBiquads = 4;
HeqSOS = []{ 0.98453370859690, -0.98453370859690, 0.98453370859690, -0.98453370859690};

Set coefficients of the H3 filter

public float[] H3Numerator;
public float[] H3Denominator;
public bool H3Enabled;
public int H3Method;
public float H3Alpha;
public int H3FilterLength;
public float H3OutputGain;

Description

These variables are used for specifying coefficients of the H3 filter.

Example

H3Numerator = []{ 0.98453370859690, -0.98453370859690, 0.98453370859690, -0.98453370859690};

H3Denominator = [] {-1.00000000000000, 0.96906741719379, -0.92300230934793, 0.89445146398370};

H3Enabled = true;
H3Method = (int)PostFilteringOptions.Alpha;
H3Alpha = 0.7;
H3FilterLength = 4;
H3OutputGain = 1.5;

Perform the data filtering operation

public float FilterData(float InputDataSample)

Description

Use this API to perform the data filtering operation.

Argument:

InputDataSample: Input data point

Example

float[] Outputbuf;

float InputDataSample = []{0.000000, 0.248566, 0.481530, 0.684268, 0.844055, 0.950859, 0.997978, 0.982454, 0.905261, 0.77124, 0.588816, 0.369427, 0.126850, -0.123690……………………};

for (int i = 0; i < InputDataSample.Length; i++)

{

Outputbuf[i] = FilterData(InputDataSample[i]);

}

Specify inputs and output math functions

public int InputMathFunction;

public int OutputMathFunction;

Description

These variables are used for specifying inputs and output math functions.

Example

InputMathFunction = (int)NLMethodOptions.TKEO;

InputMathFunction = (int)NLMethodOptions.Sqr;

Initialise the filters

public void InitialiseCascade()

Description

Initialises the filters according to specifications defined in the ASN Filter Designer software.

Reset the filter cascade

public void ResetCascade()
Description

Resets the filter cascade.