AIoT is an exciting new area that combines AI concepts (i.e. ML) with IoT in order to produce state-of-the-art smart embedded solutions. This augmentation of technologies requires a new set of tools to capture real-time IoT sensor data, analyse it, design suitable algorithms and then perform validation of the solution. After completing validation of the algorithms on the test data, a final hurdle is then how to generate efficient C code of the developed algorithm(s) for an Arm Cortex-M microcontroller for use in an application. These concepts will be discussed herein.
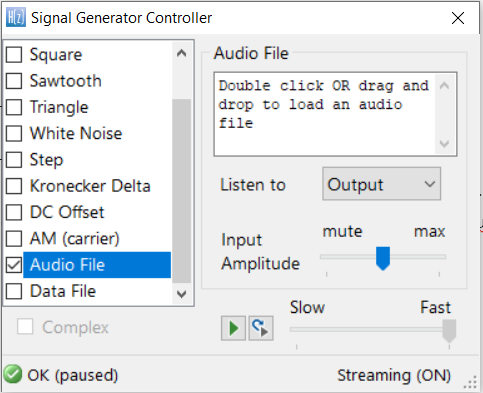
Arm’s Synchronous Data Stream (SDS) Framework provides developers with an easy method of capturing and playing back real-time sensor data for embedded AIoT sensor applications on Arm Cortex-M processors, such as ST Microelectronics’ very popular STM32 family.
The SDS Framework provides embedded developers with a variety of essential tools, such as the ability to record real-world sensor data for analysis and development in tools such as ASN Filter Designer, Python and Matlab. A set of Python utility scripts are available for recording, playback, visualisation and data conversion, where the latter supports the conversion of captured SDS data files into a single CSV file – providing a simple bridge between the ASN Filter Designer and the SDS Framework.
The SDS framework also supports the possibility to playback real-world data for algorithm validation using Arm Virtual Hardware, allowing developers to verify execution of DSP algorithms on Cortex-M targets with off-line tools.
This application note provides AIoT developers with a complete reference guide of how to develop and deploy feature extraction algorithms for use in AIoT applications to STM32 Arm Cortex-M based microcontrollers using STM32CubeIDE or Keil mVision with the Arm SDS framework and ASN Filter Designer. As mentioned above, AIoT system challenges and concepts will also be covered.
Building AIoT systems
Almost all IoT embedded sensor applications require some level of signal processing to enhance sensor data and extract features of interest. However, an obvious hurdle for many developers is how to design, test and deploy efficient algorithms for their application. This is easier said than done, as many software engineers are not well-versed in understanding the mathematical concepts needed to implement algorithms. This is further complicated by the challenge of how to implement algorithms developed by researchers that are not interested/experienced in developing real-time embedded applications.
A possible solution offered by the Mathworks (Embedded Coder) automatically translates Matlab algorithms and functions into C for Arm processors, but its high price tag and steep learning curve make it unattractive for many.
That being said, Arm and its rich ecosystem of partners provide developers with extensive easy-to-use tooling and tried and tested software libraries. Arm’s CMSIS-DSP and CMSIS-NN frameworks for algorithm development and machine learning (ML) are two very popular examples that are open source and are used internationally by tens of thousands of developers.
The Arm CMSIS-DSP software framework is particularly interesting as it provides IoT developers with a rich collection of fast mathematical and vector functions, interpolation functions, digital filtering (FIR/IIR) and adaptive filtering (LMS) functions, motor control functions (e.g. PID controller), complex math functions and supports various data types, including fixed and floating point. The important point to make here is that all of these functions have been optimised for Arm Cortex-M processors, allowing you to focus on your application rather than worrying about optimisation.
The Arm-CMSIS framework solutions are strengthened by Arm partners ASN and Qeexo who provide developers with easy-to-use real-time filtering, feature extraction (ASN Filter Designer) and ML tooling (AutoML) and reference designs, expediting the development of AIoT applications, including industrial, audio and biomedical. These solutions have been optimised for Arm processors with the help of Arm’s architecture experts and insider knowledge of compiler workings.
AIoT system building blocks
An essential pre-building block in any AIoT system is the feature extraction algorithm. The challenge for any feature extraction algorithm is to extract and enhance any relevant sensor data features in noisy or undesirable circumstances and then pass them onto the ML model in order to provide an accurate classification. The concept is illustrated below:
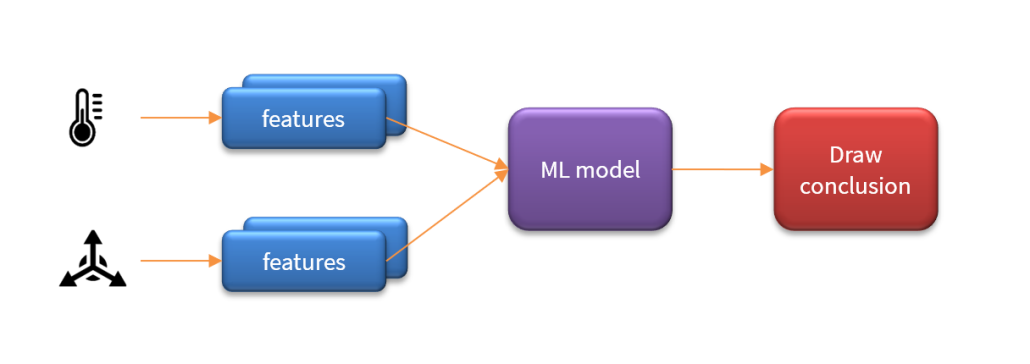
As seen above, an AIoT system may actually contain multiple feature blocks per sensor and in some cases fuse the features locally before sending them onto the ML model for classification such that the system may then draw a conclusion. The challenge is therefore how to capture sensor data for training and design suitable algorithms to extract features of interest.
Feature extraction algorithms: challenges and solutions
The challenge for any feature extraction algorithm is to extract and enhance any relevant data features in noisy data or undesirable circumstances and then pass them onto the ML model in order to provide an accurate classification. Unfortunately, many ML models perform badly, due to poor quality data and insufficient training data. An obvious challenge for AIoT is how do we obtain the training data in the first place? In many cases, this is extremely challenging as data pertaining to faults (such as preventive maintenance) is hard to come by, as many plant managers are reluctant to break their working production lines or processes to provide developers with training data.
In the absence of adequate training data, feature extraction based on science and mathematics is a prudent alternative, as less training data is required, and in general, the quality of the feature estimate is higher as knowledge of the underlying process is used. Examples include: obtaining accurate pulse and heart rate estimates from ECG and PPG sensors in smartwatch applications when a subject is moving. For industrial sensors, such as loadcells, pressure, temperature, gas and accelerometer sensors the challenge is amplified, as harsh operating conditions and the sheer variety of the applications needed for I4.0 process control applications complicate the design significantly.
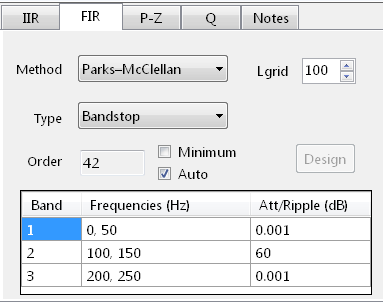
Example: Infrared gas sensor
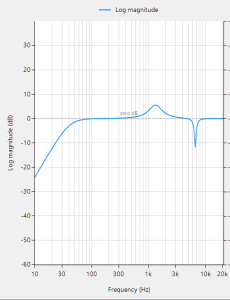
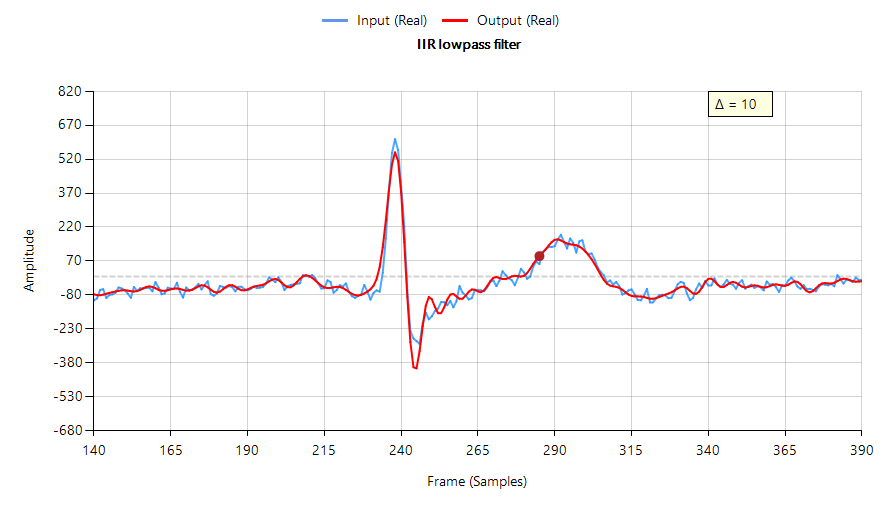
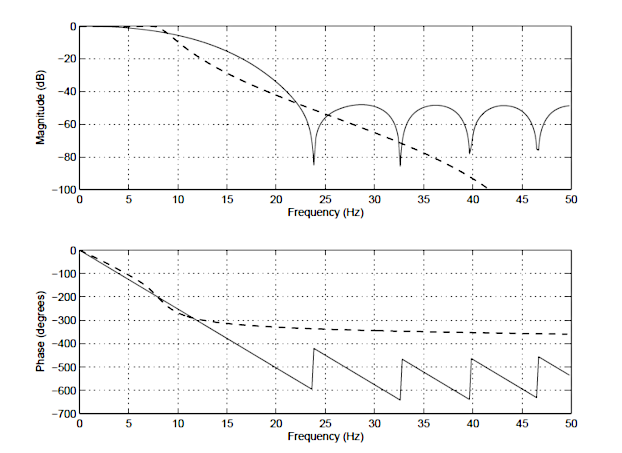
Consider the following application for gas concentration measurement from an Infrared gas sensor. The requirement is to determine the peak-to-peak amplitude of the sinusoid in order to get an estimate of gas concentration – where the bigger amplitude is the higher the gas concentration will be.
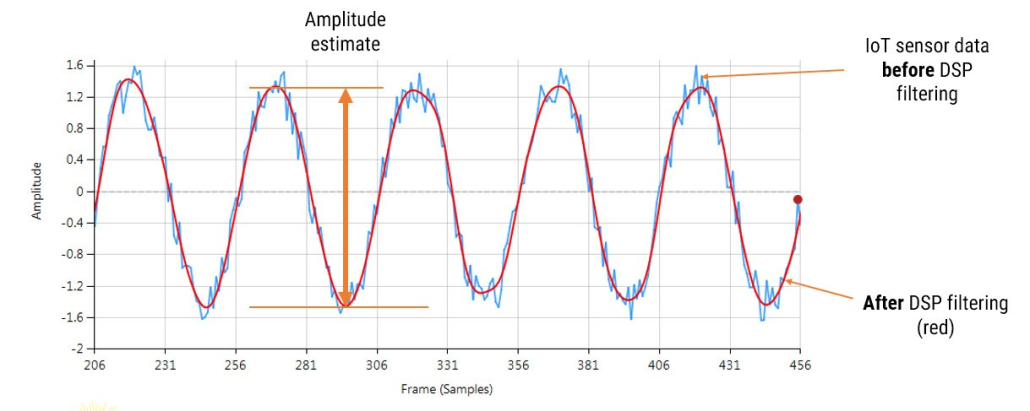
Analysing the Figure, it can be seen that the sinusoid is corrupted with measurement noise (shown in blue), and any estimate based on the blue signal will have a high degree of uncertainty about it – which is not very useful for getting an accurate reading of gas concentration! After cleaning the sinusoid with a digital filter (red line), we obtain a much more accurate and usable signal for our gas concentration estimation challenge. But how do we obtain the amplitude?
Knowing that the gradient at the peaks is zero, a relatively easy and robust way of finding the peaks of the sinusoid is via numerical differentiation, i.e. computing the difference between sample values and then looking for the zero-crossing points in the differentiated data. Armed with the positions and amplitudes of the peaks, we can take the average and easily obtain the amplitude and frequency. Notice that any DC offsets and low-frequency baseline wander will be removed via the differentiation operation.
This is just a simple example of how to extract the properties of a sinusoid in real-time using science and mathematics and an understanding of the underlying process without the need for ML training data.
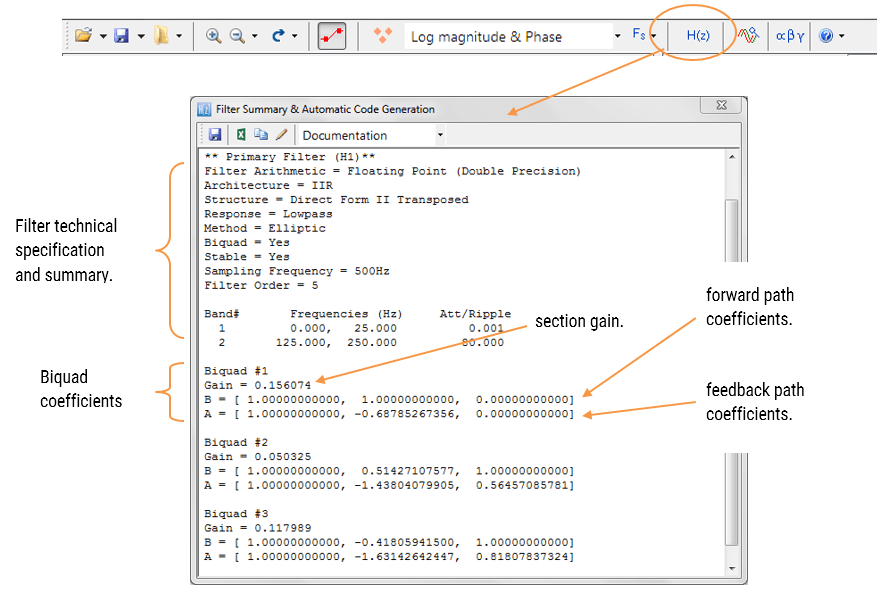
AIoT feature extraction smart sensor design workflow
Arm’s Synchronous Data Stream (SDS) Framework provides developers with an easy method of capturing and playing back real-time sensor data for embedded AIoT sensor applications on Arm Cortex-M processors. A set of Python utility scripts are available for recording, playback, visualisation and data conversion, where the latter supports the conversion of captured SDS data files into a single CSV file – providing a simple bridge between the ASN Filter Designer and the SDS Framework.
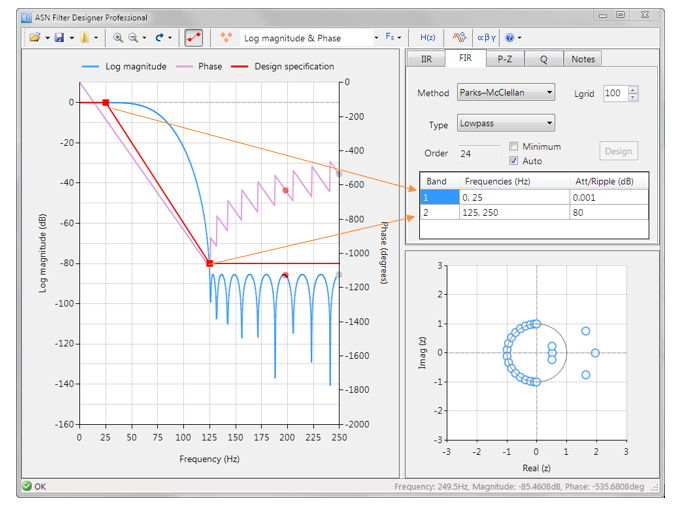
An AIoT smart sensor design workflow using the ASN Filter Designer and the SDS Framework is shown below.
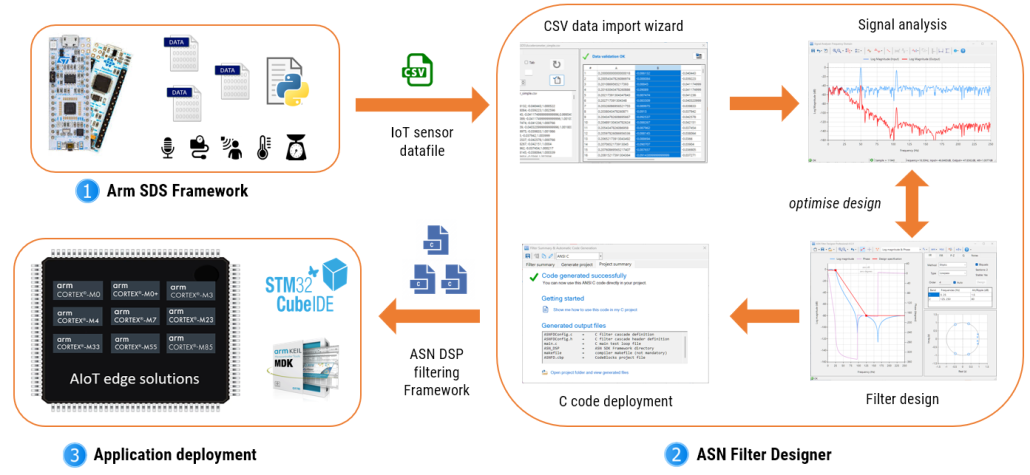
As seen above, three major components constitute the AIoT design workflow.
- Arm SDS Framework: capturing IoT sensor data and converting it to CSV format.
- ASN Filter Designer: importing the CSV datafile and then analysing the data. Based on the data analysis, a suitable filter can be designed together with other filters and IP blocks in order to build feature extraction algorithms for ML applications.
- Application deployment: Generating optimised C code and combining the design with an application for use on an Arm microcontroller.
The SDS Framework can be used with all major demo boards, including ST’s Discovery kit and Nucleo boards. SDS Python utilities are used to convert the captured *.sds and *.yaml files into a CSV file for import into the ASN Filter Designer, as discussed in the following section.
Data Import Wizard
The ASN Filter Designer’s comprehensive data import wizard can delimitate and import a variety of multi-column IoT datasets in CSV or TXT form.
As seen in the video, a generated CSV file can be dragged and dropped onto the signal analyser canvas, bringing up the data import wizard. The import wizard will automatically check the imported data for errors (such as NaNs, Infs etc) and then order the data into columns. Any header line data can be skipped by setting the Skip Headerlines value respectively.
For the example considered herein, the data is actually triaxial accelerometer data (i.e. X, Y and Z axes) with an extra column for the timebase. Therefore, if we wish to import the X-axis data, we can simply click on the header for the second column (B). The tool will then ask you to recheck the data, and upon clicking on ‘Save’ will save the selected data as a single-column CSV file (needed for the ASN Filter Designer). This new CSV file can then be streamed via the tool’s signal generator for algorithm development.
Deploying to Arm Cortex-M processors
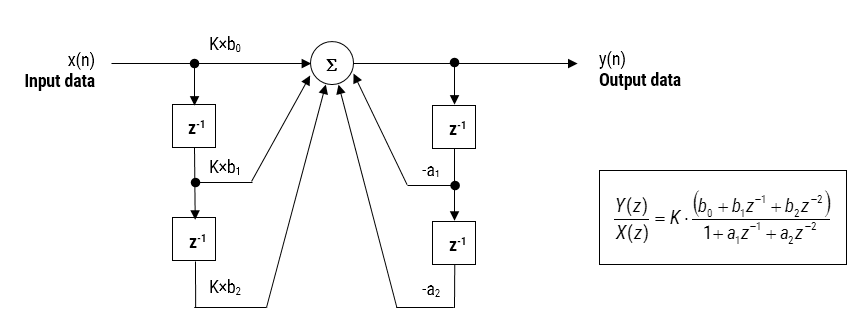
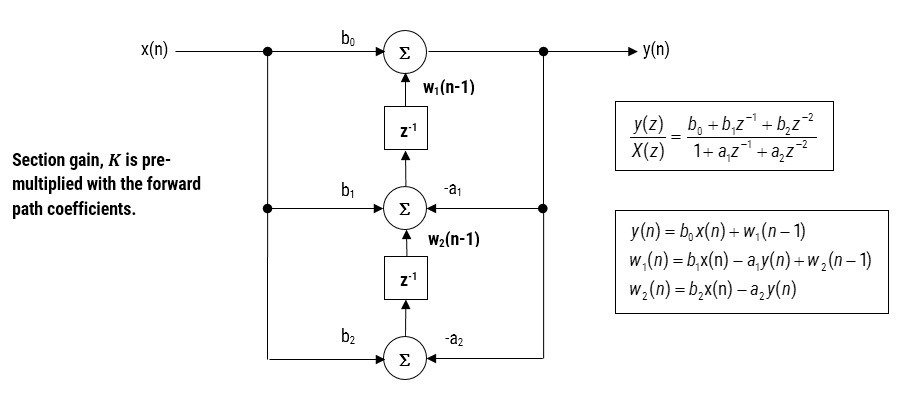
After completing the design process, the designed filter(s) can be deployed to STM32CubeIDE or Arm/Keil uVision for integration into an application project. Depending on the functionality of the ASN Filter Designer’s signal chain, two software frameworks are available: Arm’s CMSIS-DSP and ASN’s ANSI C DSP.
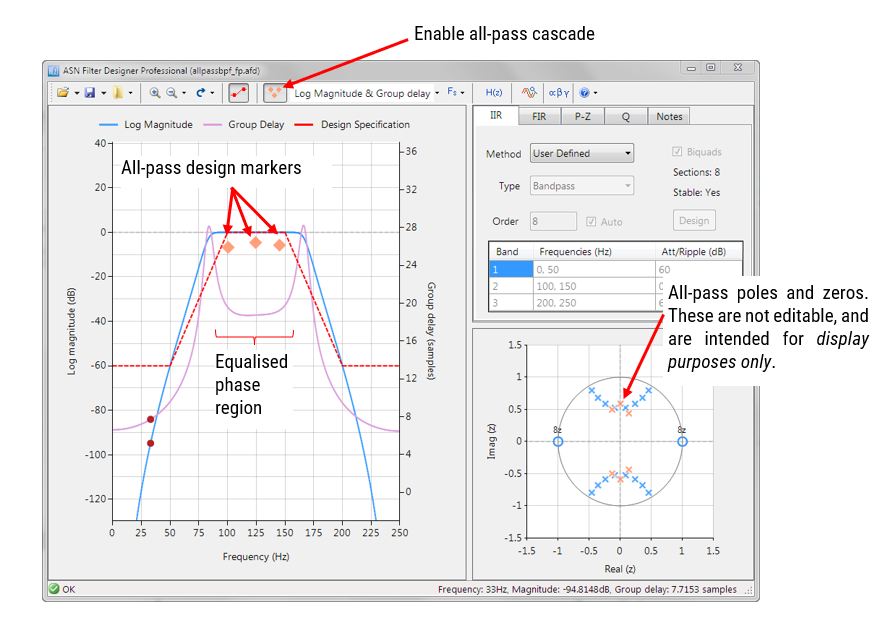
The ANSI C DSP framework was developed with close collaboration with Arm’s architecture team, providing outstanding computational performance that is required for real or complex coefficient floating-point designs that use multiple filters and mathematical functions in a signal chain. The Arm CMSIS-DSP framework on the other hand is an excellent choice for implementing both fixed-point and floating-point filters, but is limited to real coefficient single FIR filter or one IIR Biquad cascade with no extra mathematical functions.
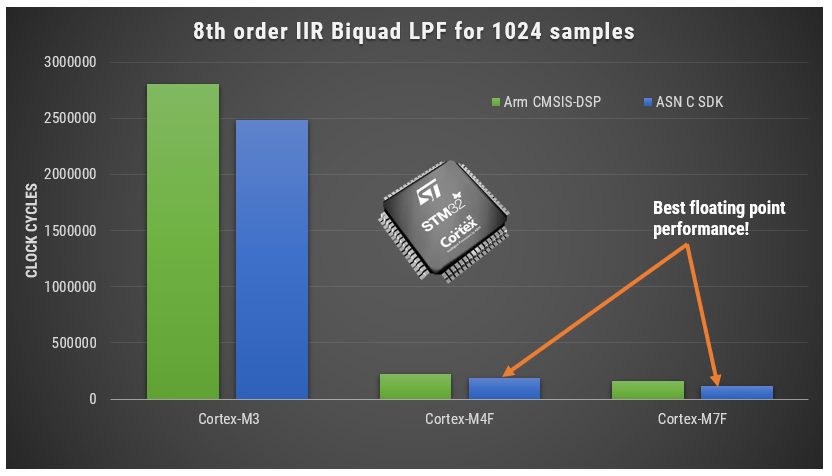
A benchmark comparison for both frameworks is shown below for an 8th IIR filter running on three different Arm cores. As seen, the ASN Framework is slightly faster (lower means better performance) than the Arm Framework.
Arm CMSIS-DSP wizard
Professional licence users may expedite the deployment by using the Arm deployment wizard. The tool will automatically analyse your design and choose a suitable Framework. If the design cannot be exported via the Arm CMSIS-DSP framework, the tool will suggest that you use the ASN ANSI C framework and launch the code generation wizard.
Note that the built-in AI will automatically determine the best settings for your design based on the quantisation settings chosen.
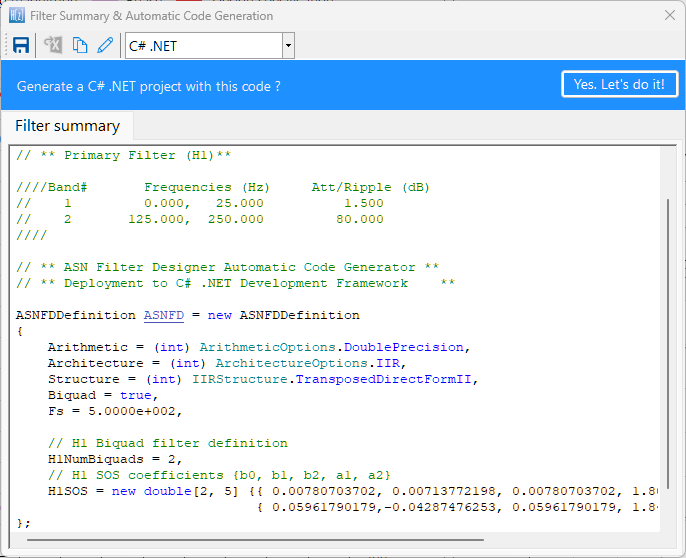
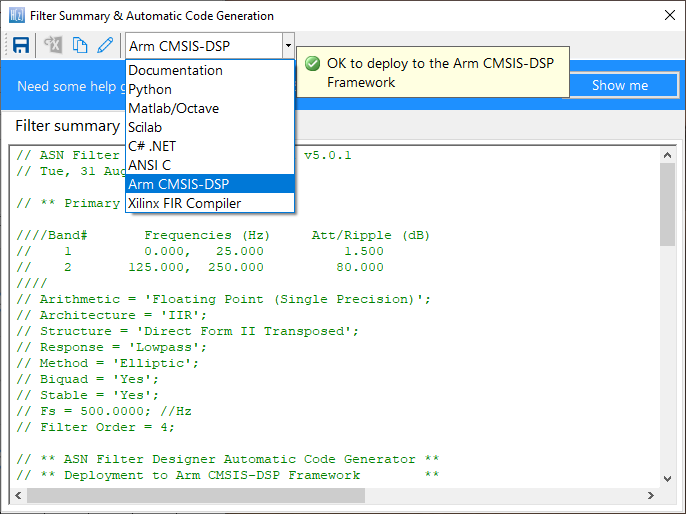
Clicking on Deploy will automatically analyse your complete filter cascade and convert any extra filters in the cascade into an H1 (primary) for implementation. Upon completion, the tool will then launch the C code generation wizard.
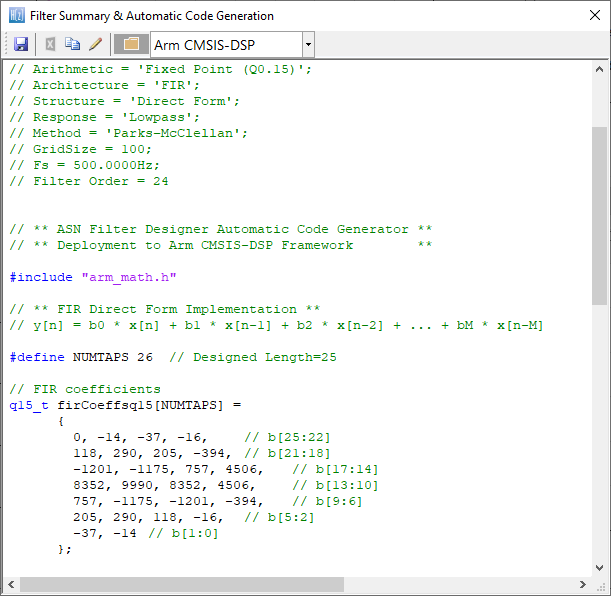
CMSIS-DSP C code generation
Depending on which C framework is used, the C code generator wizard will automatically generate the C code needed for your design. For developers using the Arm CMSIS-DSP framework, a single C file is generated for use with an MDK5 software pack. The MDK5 pack is available from Arm Keil’s software pack repository, providing several complete filtering examples based on the ASN Filter Designer’s code generator using the Arm CMSIS-DSP library.
A detailed help tutorial is available by clicking on the Show me button.
ASN ANSI C DSP code generation
For developers using the ASN ANSI C DSP framework, the code wizard should be used.
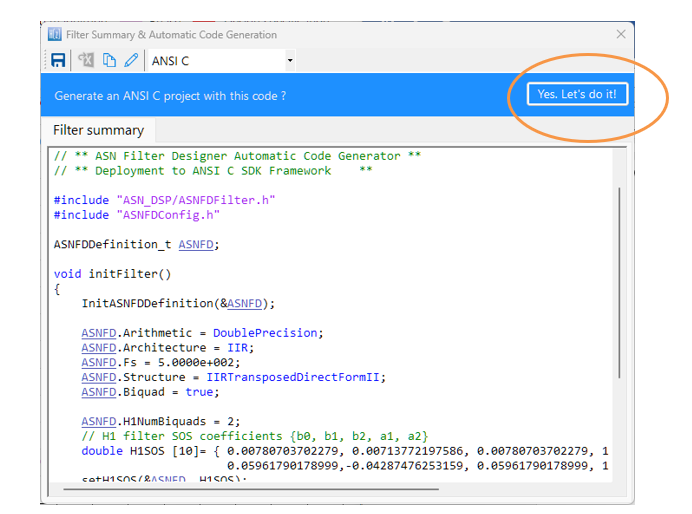
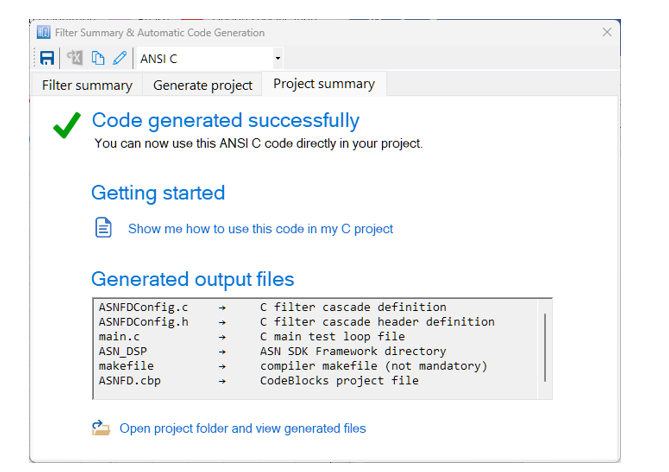
NB. The wizard will produce a CodeBlocks project in order to get you started. The following section describes in detail the steps needed for using the generated code in a STM32CUBE-IDE project. Please refer to the ANSI C SDK user guide for step-by-step instructions on how to use the generated code in other IDEs.
A PDF version of this article is available as an application note.