Obwohl der Entwurf von FIR-Filtern mit linearer Phase eine einfache Aufgabe ist, gilt dies sicherlich nicht für IIR-Filter, die in der Regel einen stark nichtlinearen Phasengang aufweisen, insbesondere um die Grenzfrequenzen des Filters. In diesem Artikel werden die Eigenschaften besprochen, die ein digitales Filter benötigt, um eine lineare Phase zu haben, und wie die Durchlassphase eines IIR-Filters modifiziert werden kann, um eine lineare Phase mit Allpass-Entzerrungsfilter zu erreichen.
Warum brauchen wir linearphasige Filter?
Digitale Filter mit linearer Phase haben den Vorteil, dass sie alle Frequenzkomponenten um den gleichen Betrag verzögern, d. h. sie erhalten die Phasenbeziehungen des Eingangssignals. Diese Erhaltung der Phase bedeutet, dass das gefilterte Signal die Form des ursprünglichen Eingangssignals beibehält. Diese Eigenschaft ist für Audioanwendungen essentiell, da die Signalform entscheidend für die Beibehaltung einer hohen Wiedergabetreue im gefilterten Audiosignal ist. Ein weiterer Anwendungsbereich, der dies erfordert, ist die biomedizinische EKG-Wellenformanalyse, da jegliche Artefakte, die durch den Filter eingeführt werden, als Herzanomalien fehlinterpretiert werden können.
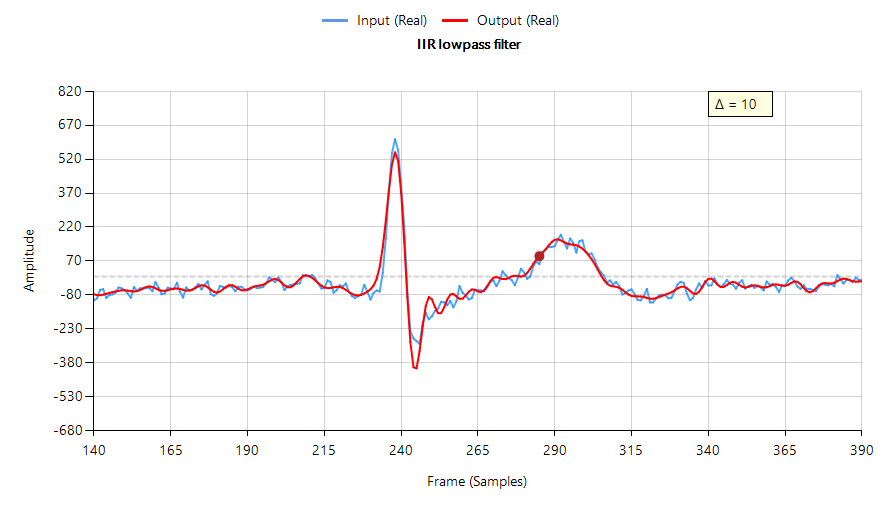
Das folgende Diagramm zeigt die Filterleistung eines Tschebyscheff-Typ-I-Tiefpasses auf EKG-Daten – die Eingangswellenform (in blau dargestellt) wurde um 10 Samples (\(\small \Delta=10\)) verschoben, um die Gruppenlaufzeit des Filters annähernd zu kompensieren. Beachten Sie, dass das gefilterte Signal (in rot dargestellt) abgeschwächt, verbreitert und mit Oszillationen um den EKG-Peak versehen ist, was unerwünscht ist.
Damit ein digitales Filter eine lineare Phase hat, muss seine Impulsantwort eine konjugiert-gerade oder konjugiert-ungerade Symmetrie um ihren Mittelpunkt haben. Dies ist für ein FIR-Filter leicht zu erkennen,
Mit der folgenden Einschränkung für seine Koeffizienten,
was dazu führt,
Die Analyse von Gl. 3 zeigt, dass die Wurzeln (Nullstellen) von \(\small H(z)\) auch die Nullstellen von \(\small H^\ast (1/z^\ast)\)sein müssen. Das bedeutet, dass die Wurzeln von \(\small H(z)\) in konjugierten reziproken Paaren auftreten müssen, d. h. wenn \(\small z_k\) eine Nullstelle von \(\small H(z)\) ist, dann muss auch \(\small H^\ast (1/z^\ast)\) eine Nullstelle sein.
Warum IIR-Filter keine lineare Phase haben
Ein digitales Filter wird als “bounded input, bounded output stable” oder “BIBO stable” bezeichnet, wenn jede gebundene Eingabe zu einer gebundenen Ausgabe führt. Alle IIR-Filter haben entweder Pole oder sowohl Pole als auch Nullstellen und müssen BIBO-stabil sein, d. h.
\(\displaystyle \sum_{k=0}^{\infty}\left|h(k)\right|<\infty \tag{4}\)
Dabei ist \(\small h(k)\) die Impulsantwort des Filters. Bei der Analyse von Gl. 4 sollte klar sein, dass das BIBO-Stabilitätskriterium nur dann erfüllt ist, wenn die Pole des Systems innerhalb des Einheitskreises liegen, da die ROC (Region der Konvergenz) des Systems den Einheitskreis einschließen muss. Folglich ist es ausreichend zu sagen, dass ein begrenztes Eingangssignal immer ein begrenztes Ausgangssignal erzeugt, wenn alle Pole innerhalb des Einheitskreises liegen.
Die Nullstellen hingegen sind nicht durch diese Anforderung eingeschränkt und können folglich überall auf der z-Ebene liegen, da sie die Systemstabilität nicht direkt beeinflussen. Daher kann eine Systemstabilitätsanalyse durchgeführt werden, indem zunächst die Wurzeln der Übertragungsfunktion (d. h. die Wurzeln der Zähler- und Nennerpolynome) berechnet werden und dann die entsprechenden Pole und Nullstellen auf der z-Ebene aufgetragen werden.
Wendet man die entwickelte Logik auf die Pole eines IIR-Filters an, kommt man nun zu einer sehr wichtigen Schlussfolgerung, warum IIR-Filter keine lineare Phase haben können.
Ein BIBO-stabiles Filter muss seine Pole innerhalb des Einheitskreises haben, und um eine lineare Phase zu erhalten, müsste ein IIR-Filter konjugierte reziproke Pole außerhalb des Einheitskreises haben, was es BIBO-instabil macht.
Basierend auf dieser Aussage scheint es nicht möglich zu sein, einen IIR so zu konstruieren, dass er eine lineare Phase hat. Wie unten beschrieben, können jedoch Phasenentzerrungsfilter verwendet werden, um den Phasengang des Durchlassbereichs zu linearisieren.
Phasenlinearisierung mit Allpassfiltern
All-pass phase linearisation filters (equalisers) (Equalizer) sind eine gut etablierte Methode, um den Phasengang eines Filters zu ändern, ohne den Betragsgang zu beeinflussen. Ein Allpassfilter zweiter Ordnung (Biquad) ist definiert als:
Dabei ist\(\small f_c\) die Mittenfrequenz, \(\small r\) der Radius der Pole und \(\small f_s\) die Abtastfrequenz. Beachten Sie, dass die Koeffizienten von Zähler und Nenner als spiegelbildliches Paar zueinander angeordnet sind. Die Spiegeleigenschaft ist es, die dem Allpassfilter seine wünschenswerte Eigenschaft verleiht, nämlich dem Konstrukteur zu ermöglichen, den Phasengang zu verändern, während der Betragsgang über das gesamte Frequenzspektrum konstant oder flach bleibt.
Wenn man eine APF-Entzerrungskaskade (bestehend aus mehreren APFs) mit einem IIR-Filter kaskadiert, besteht die Grundidee darin, dass man nur den Phasengang im Durchlassbereich linearisieren muss. Die anderen Bereiche, wie z. B. das Übergangsband und das Sperrband, können ignoriert werden, da jegliche Nichtlinearitäten in diesen Bereichen für das Gesamtergebnis der Filterung von geringem Interesse sind.
Die Herausforderung
Die APF-Kaskade klingt wie ein idealer Kompromiss für diese Herausforderung, aber in Wahrheit ist ein erheblicher Zeitaufwand und eine sehr sorgfältige Feinabstimmung der APF-Positionen erforderlich, um ein akzeptables Ergebnis zu erzielen. Jeder APF hat zwei Variablen \(\small f_c\) und \(\small r\) , die optimiert werden müssen, was die Lösung verkompliziert. Erschwerend kommt hinzu, dass die Gruppenverzögerung (Latenz) des Gesamtfilters umso höher wird, je mehr APF-Stufen zur Kaskade hinzugefügt werden. Letzteres kann für schnelle Echtzeit-Regelsysteme, die sich auf die niedrige Latenzzeit eines IIR-Filters verlassen, problematisch werden.
Trotz dieser Herausforderungen ist der APF-Equalizer ein guter Kompromiss für die Linearisierung der Durchlassband-Phaseneigenschaften eines IIR-Filters.
Der APF-Entzerrer
Der ASN Filter Designer bietet Entwicklern eine sehr einfach zu bedienende grafische All-Phase-Equalizer-Oberfläche für die Linearisierung der Durchlassbandphase von IIR-Filtern. Wie unten zu sehen ist, ist die Oberfläche sehr intuitiv und erlaubt es dem Designer, APF-Filterpositionen schnell mit der Maus zu platzieren und fein abzustimmen. Das Werkzeug berechnet automatisch \(\small f_c\) und \(\small r\), basierend auf der Markerposition.
APF-Equalizer ASN Filter Designer
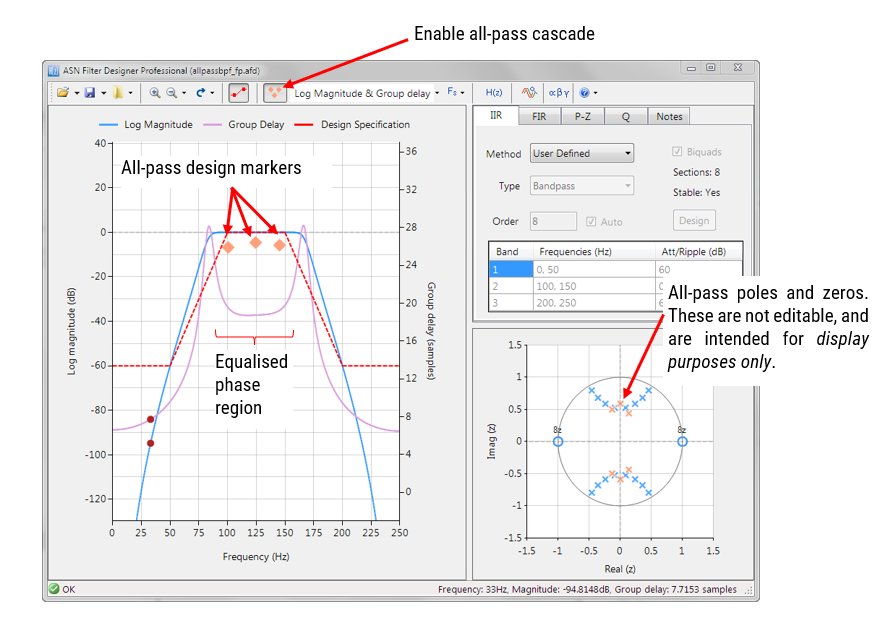
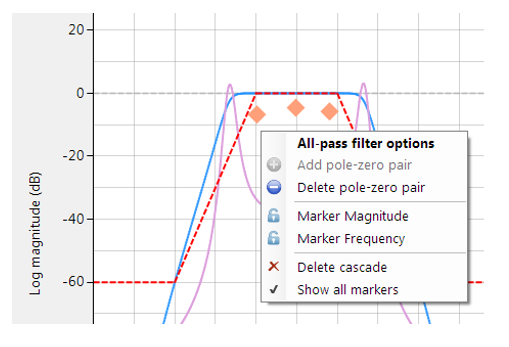
Wenn Sie mit der rechten Maustaste auf das Frequenzgangdiagramm oder auf einen vorhandenen Allpass-Design-Marker klicken, wird ein Optionsmenü angezeigt, wie links dargestellt.
Sie können bis zu 10 Biquads hinzufügen (nur professionelle Version).
Ein IIR mit linearer Phase im Durchlaßbereich
Wenn wir einen Equalizer entwerfen, der aus drei APF-Paaren besteht, und ihn mit dem Tschebyscheff-Filter aus Abbildung 1 kaskadieren, erhalten wir eine Filterwellenform, die eine viel schärfere Spitze mit weniger Dämpfung und Oszillation als der ursprüngliche IIR hat – siehe unten. Diese Verbesserung geht jedoch auf Kosten von drei zusätzlichen Biquad-Filtern (der APF-Kaskade) und einer erhöhten Gruppenlaufzeit, die nun auf 24 Samples im Vergleich zu den ursprünglichen 10 Samples angestiegen ist.
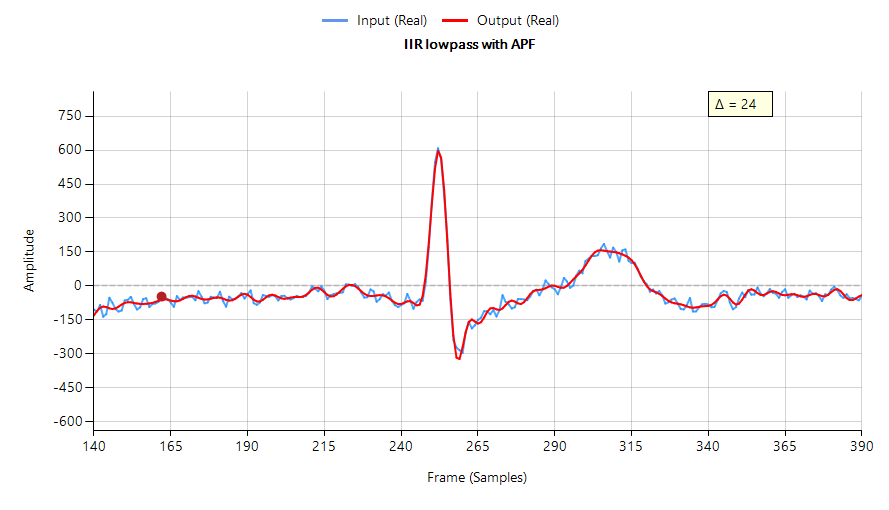
(minimale Phasenverzerrung)
Der Frequenzgang sowohl des ursprünglichen IIR als auch des entzerrten IIR ist unten dargestellt, wobei die Gruppenverzögerung (in lila dargestellt) die durchschnittliche Verzögerung des Filters ist und eine einfachere Methode zur Beurteilung der Linearität darstellt.
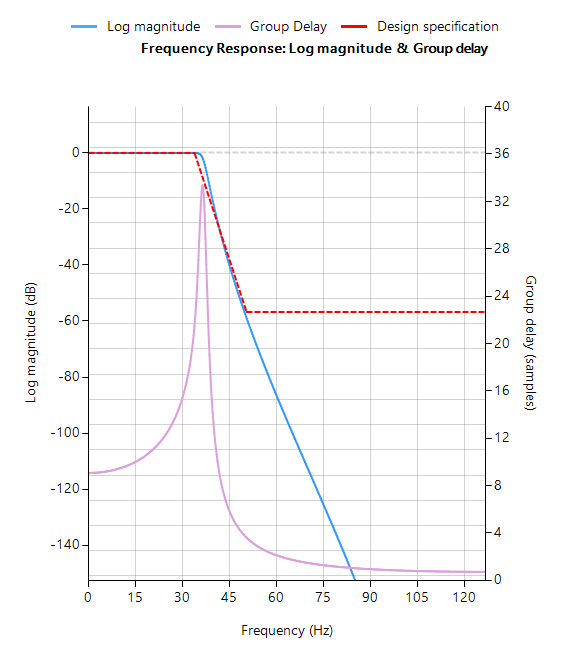
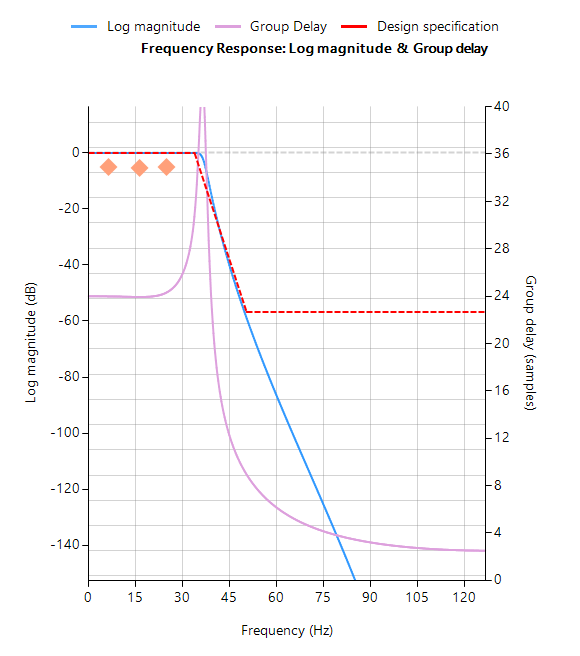
Beachten Sie, dass die Gruppenlaufzeit des entzerrten IIR-Durchlassbereichs (rechts dargestellt) fast flach ist, was bestätigt, dass die Phase tatsächlich linear ist.
Automatische Code-Generierung für Arm-Prozessorkerne über CMSIS-DSP
Die automatische Code-Generierung des ASN Filter Designers erleichtert den Export eines entworfenen Filters auf Cortex-M Arm basierte Prozessoren über das CMSIS-DSP Software-Framework. Die integrierten Analyse- und Hilfefunktionen des Tools unterstützen den Designer bei der erfolgreichen Konfiguration des Designs für den Einsatz.
Vor der Generierung des Codes müssen die IIR- und Entzerrungsfilter (d. h. H1- und Heq-Filter) zunächst zu einer H1-Filterstruktur (Hauptfilter) für den Einsatz reoptimiert (zusammengeführt) werden. Das Optionsmenü befindet sich unter der Registerkarte P-Z in der Haupt-Benutzeroberfläche.
Alle Entwürfe von Fließkomma-IIR-Filtern müssen auf Single-Precision-Arithmetik und entweder auf einer Direct Form I- oder Direct Form II-Transposed-Filterstruktur basieren. Die Direct Form II Transposed-Struktur wird aufgrund ihrer höheren numerischen Genauigkeit für die Fließkomma-Implementierung befürwortet.
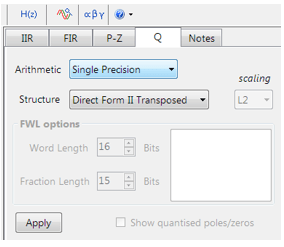
Die Einstellungen für Quantisierung und Filterstruktur finden Sie unter der Registerkarte Q (wie links dargestellt). Durch Einstellen von Arithmetic auf Single Precision und Structure auf Direct Form II Transposed und Klicken auf die Schaltfläche Apply wird die hier betrachtete IIR für das Software-Framework CMSIS-DSP konfiguriert.
Wählen Sie das Arm CMSIS-DSP-Framework aus der Auswahlbox im Filterübersichtsfenster aus:
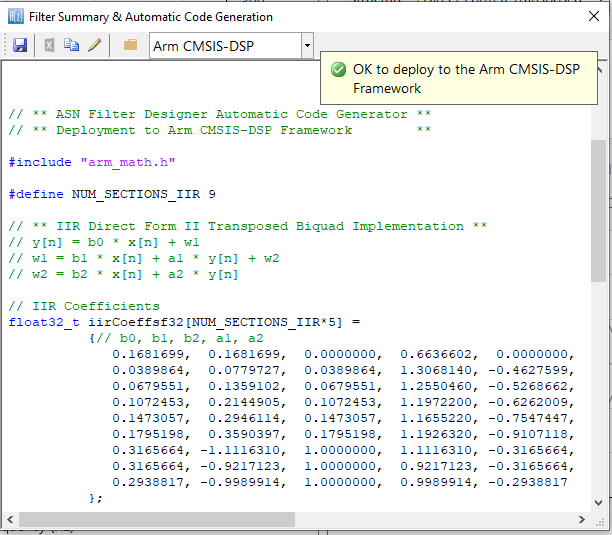
Der automatisch generierte C-Code auf Basis des CMSIS-DSP-Frameworks für die direkte Implementierung auf einem Arm-basierten Cortex-M-Prozessor ist unten dargestellt:
Der automatische Code-Generator des ASN Filter Designers generiert den gesamten Initialisierungscode, die Skalierung und die Datenstrukturen, die für die Implementierung des linearisierten IIR-Filters über die CMSIS-DSP-Bibliothek von Arm benötigt werden.
Was wir gelernt haben
Die Wurzeln eines linearphasigen Digitalfilters müssen in konjugierten reziproken Paaren auftreten. Obwohl dies für ein FIR-Filter kein Problem ist, wird es für ein IIR-Filter undurchführbar, da die Pole sowohl innerhalb als auch außerhalb des Einheitskreises liegen müssten, was das Filter BIBO-instabil macht.
Der Durchlassbereich-Phasengang eines IIR-Filters kann mit Hilfe einer APF-Entzerrungskaskade linearisiert werden. Der ASN Filter Designer bietet dem Entwickler über eine sehr einfach zu bedienende, grafische Allpass-Phasenentzerrer-Oberfläche alles, was er braucht, um eine geeignete APF-Kaskade nur mit der Maus zu entwerfen!
Das linearisierte IIR-Filter kann über den automatischen Code-Generator unter Verwendung der optimierten CMSIS-DSP-Bibliotheksfunktionen von Arm für den Einsatz auf jedem Cortex-M-Mikrocontroller exportiert werden.