Butterworth Filter
Syntax
Hd = butter (Order, Frequencies, Rp, Rs, Type, DFormat)
Description
Classic IIR Butterworth filter design
- Smooth monotonic response (no ripple)
- Slowest roll-off for equivalent order
- Highest order of all supported prototypes
Order: may be specified up to 20 (professional) and up to 10 (educational) edition. Setting the Order to 0, enables the automatic order determination algorithm.
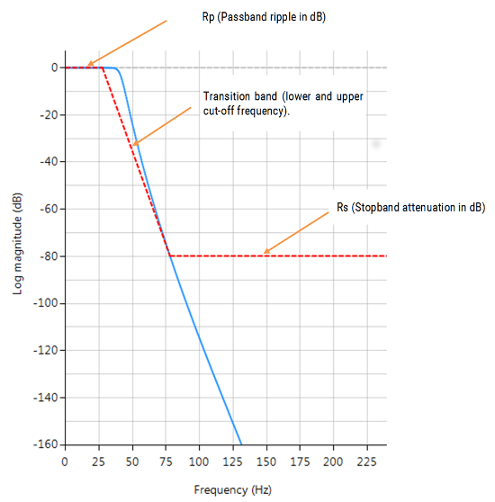
Frequencies: lowpass and highpass filters have one transition band, and in as such require two frequencies (i.e. lower and upper cut-off frequencies of the transition band). For bandpass and bandstop filters, four frequencies are required (i.e. two transition bands). All frequencies must be ascending in order and < Nyquist (see the example below). Rp: Passband ripple in dB. This is somewhat of a misnomer, as the Butterworth filter has a maximally flat passband. A good default value is 0.001dB, but increasing this value will affect the position of the filter’s lower cut-off frequency.
Rs: Stopband attenuation in dB. This is somewhat of a misnomer, as the Butterworth filter has a maximally flat stopband, which means that the stopband attenuation (assuming the correct filter order is specified) will be ≥ stopband specification.
Type: The Butterworth method facilitates the design of lowpass, highpass, bandpass and bandstop filters respectively.
Hd: the Butterworth method designs an IIR Butterworth filter based on the entered specifications and places the transfer function (i.e. numerator, denominator, gain) into a digital filter object, Hd. The digital filter object can then be combined with other methods if so required. For a digital filter object, Hd, calling getnum(Hd), getden(Hd) and getgain(Hd) will extract the numerator, denominator and gain coefficients respectively – see below.
DFormat: allows you to specify the display format of resulting digital filter object.
symbolic |
Display a symbolic representation of the filter object. If the order > 10, the symbolic display option will be overridden and set to numeric |
numeric |
Display a matrix representation of the filter object |
void |
Create a filter object, but do not display output |
Example
[code lang=”java”]
ClearH1; // clear primary filter from cascade
ShowH2DM; // show DM on chart
Main()
Rp=0.001;
Rs=80;
F={50,120};
Hd=butter(0,F,Rp,Rs,”lowpass”,”symbolic”);
F={50,80,100,120};
Hd=butter(0,F,Rp,Rs,”bandpass”,”symbolic”);
Num = getnum(Hd); // define numerator coefficients
Den = getden(Hd); // define denominator coefficients
Gain = getgain(Hd); // define gain [/code]
See also
bessel / butter / cheby1 / cheby2 / ellip / arbmagphase / cplxfreqshift / dcremover / notch / peaking