Kamfilters (Combfilters) worden gebruikt als powerline (50/60Hz) harmonische annuleringsfilters in audiotoepassingen, en vormen de basis van zogenaamde CIC (cascaded integrator-comb) filters. Deze worden gebruikt voor anti-aliasing in decimatie (sample rate reductie), en anti-imaging in interpolatie (sample rate toename) toepassingen.
De frequentierespons van een kamfilter bestaat uit een reeks van op regelmatige afstand van elkaar geplaatste dalen, die het uiterlijk van een kam geven. Zoals te zien in onderstaande grafiek, verschijnt de afstand van elk dal op oneven of zelfs harmonisch van de gewenste grondfrequentie.
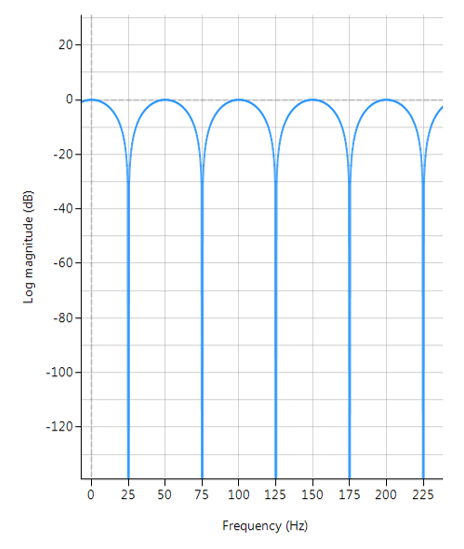
Frequentierespons van een typische FIR-kamfilter (oneven harmonieën):
\(f_s=500Hz\), \(f_c=25Hz\), \(L=10\) and \(\alpha=1\)
Een FIR-kamfilter kan worden beschreven met de volgende transferfunctie:
\(H(z)=1+\alpha z^{-L}\)
\(\Rightarrow Y(z)=X(z)\left[1+\alpha z^{-L}\right]\)
Het is duidelijk dat de kamfilter gewoon een gewogen vertraagde replica van zichzelf is, gespecificeerd door \(L\). Door het nemen van inverse z-transformaties krijgen we de verschilvergelijking die nodig is voor de implementatie,
\(y(n)=x(n)+\alpha x(n-L)\)Waarbij \(\alpha\) wordt gebruikt om de Q (bandbreedte) van de notch in te stellen. Deze kan zowel positief als negatief zijn, afhankelijk van het soort frequentierespons dat nodig is. Negatieve waarden van \(\alpha\) hebben hun eerste dieptepunt bij DC en hun tweede dieptepunt bij de fundamentele frequentie. Het is duidelijk dat dit type kamfilter gebruikt kan worden om eventuele DC-componenten uit een gemeten golfvorm te verwijderen als dat nodig is. Alle volgende dalen verschijnen bij gelijkmatige harmonische tot en met de Nyquist-frequentie.
Aan de andere kant hebben positieve waardes van \(\alpha\) alleen op de fundamentele en oneven harmonische frequenties, en kan als zodanig niet worden gebruikt om eventuele DC-componenten te verwijderen.
Toepassing op storingsonderdrukking van de stroomlijn
De affectiviteit van het kamfilter is afhankelijk van de sampling frequency, \(f_s\), aangezien \(L\) alleen beperkt is tot gehele waarden. Ook is een relatie tussen \(f_s\), als \(L\), afhankelijk van het teken van \(\alpha\). In het kader van de in deze discussie besproken toepassing van de netbeëindiging zullen dus alleen positieve waarden van de harmonics in aanmerking worden genomen, aangezien we alleen oneven harmonics hoeven te annuleren.
Een simpele relatie om \(L\) te bepalen kan als volgt worden samengevat voor positieve waardes van\(\alpha\):
\(L=ceil\left( \large{\frac{f_s}{2f_c}}\right)\)Waarbij \(f_c\) het gewenste middelpunt is van de fundamentele notch frequentie. Op basis van deze uitdrukking kunnen we de sample frequentie herberekenen op dusdanige wijze dat \(f_c\) een echt veelvoud is van \(f_s\)
\(f_{snew}=2f_c L\)Voorbeeld van een kamfilter
Voor het hier besproken voorbeeld, d.w.z. \(f_s=500Hz\) en \(f_c=25Hz\), verkrijgen we \(L=10\). Echter, als \(f_c=60Hz\), zouden we \(L=5\) nodig hebben en een nieuwe sampling rate van \(600Hz\). Hoewel het interessant is om op te merken dat \(f_s=480Hz\) voor \(L=4\) ook voldoende zou zijn.
Implementatie
Een FIR kamfilter kan als volgt in ASN FilterScript worden geimplementeerd:
ClearH1; // clear primary filter from cascade
interface L = {4,20,1,5}; // delay
interface alpha = {-1,1,0.01,1};
Main()
Num = {1,zeros(L-1),alpha}; // numerator coefficients
Den = {1};
Gain = 1/sum(abs(Num));


Leave a Reply
Want to join the discussion?Feel free to contribute!