Klassischer IIR-Filterentwurf: ein praktischer Leitfaden

IIR-Filter (unendliche Impulsantwort) werden im Allgemeinen für Anwendungen gewählt, bei denen die lineare Phase nicht allzu wichtig ist und der Speicherplatz begrenzt ist. Sie werden häufig bei der Audio-Entzerrung, der Signalverarbeitung von biomedizinischen Sensoren, intelligenten IoT/IIoT-Sensoren und Hochgeschwindigkeits-Telekommunikations-/RF-Anwendungen eingesetzt und bilden einen entscheidenden Baustein im algorithmischen Design. Ein praktischer Leitfaden für die am häufigsten verwendeten oder klassischen IIR-Digitalfilter-Entwurfsmethoden: Butterworth, Tschebyscheff Typ I, Tschebyscheff Typ II und Elliptisch

Vorteile

• Geringer Implementierungsaufwand: benötigt weniger Koeffizienten und Speicher als FIR-Filter, um einen ähnlichen Satz an Spezifikationen zu erfüllen, d. h. Grenzfrequenz und Stoppbanddämpfung
• Geringe Latenz: geeignet für Echtzeit-Steuerung und sehr schnelle HF-Anwendungen aufgrund des geringen Koeffizienten-Footprints
• Kann zur Nachahmung der Eigenschaften von analogen Filtern unter Verwendung von s-z-Ebenen-Mapping-Transformationen verwendet werden

Nachteile

• Nichtlineare Phaseneigenschaften
• Erfordert mehr Skalierung und numerische Überlaufanalyse, wenn in Festkomma implementiert
• Aufgrund der Rückkopplungspfade weniger numerisch stabil als ihre FIR-Pendants (Finite-Impulse-Response)

Definition

Ein IIR-Filter wird durch seine theoretisch unendliche Impulsantwort kategorisiert,

\(\displaystyle
y(n)=\sum_{k=0}^{\infty}h(k)x(n-k)
\)

Praktisch gesehen ist es nicht möglich, den Ausgang eines IIR mit dieser Gleichung zu berechnen. Daher kann die Gleichung in Form einer endlichen Anzahl von Polen \(p\) und Nullstellen \(q\)umgeschrieben werden, wie durch die lineare Differenzgleichung mit konstantem Koeffizienten definiert, die wie folgt lautet

\(\displaystyle
y(n)=\sum_{k=0}^{q}b(k)x(n-k)-\sum_{k=1}^{p}a(k)y(n-k)
\)

wobei \(a(k)\) und \(b(k)\) die Nenner- und Zähler-Polynomkoeffizienten des Filters sind, deren Wurzeln gleich den Polen bzw. Nullstellen des Filters sind. Daher kann eine Beziehung zwischen der Differenzengleichung und der z-Transformation (Übertragungsfunktion) unter Verwendung der Verzögerungseigenschaft der z-Transformation so definiert werden, dass,

\(\displaystyle
\sum_{k=0}^{q}b(k)x(n-k)-\sum_{k=1}^{p}a(k)y(n-k)\quad\stackrel{\displaystyle\mathcal{Z}}{\longleftrightarrow}\quad\frac{\sum\limits_{k=0}^q b(k)z^{-k}}{1+\sum\limits_{k=1}^p a(k)z^{-k}}
\)

Wie Sie sehen, ist die Übertragungsfunktion eine Frequenzbereichsdarstellung des Filters. Beachten Sie auch, dass die Pole auf die Ausgangsdaten wirken und die Nullen auf die Eingangsdaten. Da die Pole auf die Ausgangsdaten wirken und die Stabilität beeinflussen, ist es für die BIBO-Stabilität (bounded input, bounded output) wichtig, dass ihre Radien innerhalb des Einheitskreises bleiben (d. h. <1). Die Radien der Nullstellen sind weniger kritisch, da sie die Stabilität des Filters nicht beeinflussen. Dies ist der Hauptgrund, warum FIR-Filter (endliche Impulsantwort) mit nur Nullen immer stabil sind.

Eine Diskussion von IIR-Filterstrukturen sowohl für Festkomma als auch für Fließkomma finden Sie hier.

Klassische IIR-Entwurfsmethoden

Es folgt nun eine Diskussion der am häufigsten verwendeten oder klassischen IIR-Entwurfsmethoden (Butterworth, Tschebyscheff und Elliptisch). Wer nach allgemeineren Beispielen sucht, findet im ASN-Blog viele Artikel zu diesem Thema.

Wie unten beschrieben, hat jede Methode ihre Vor- und Nachteile, aber im Allgemeinen sollte die elliptische Methode als erste Wahl betrachtet werden, da sie die Entwurfsspezifikationen mit der niedrigsten Ordnung aller Methoden erfüllt. Diese wünschenswerte Eigenschaft geht jedoch auf Kosten der Welligkeit sowohl im Durchlass- als auch im Sperrbereich und der sehr nichtlinearen Durchlassband-Phaseneigenschaften. Daher sollte das elliptische Filter nur in Anwendungen eingesetzt werden, bei denen der Speicherplatz begrenzt ist und die Linearität der Durchlassphase weniger wichtig ist.

Die Butterworth- und Tschebyscheff-Typ-II-Methoden haben flache Durchlassbänder (keine Welligkeit), was sie zu einer guten Wahl für DC- und Niederfrequenz-Messanwendungen macht, wie z. B. Brückensensoren (z. B. Kraftmesszellen). Diese wünschenswerte Eigenschaft geht jedoch auf Kosten breiterer Übergangsbänder, was zu einem niedrigen Übergang vom Durchlass- zum Sperrbereich führt (langsamer Roll-Off). Die Tschebyscheff-Methode Typ I und die elliptische Methode rollen schneller ab, haben aber eine Durchlassband-Welligkeit und eine sehr nichtlineare Durchlassband-Phasenkennlinie.

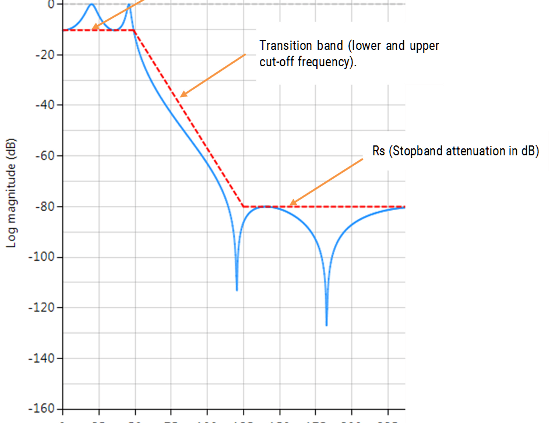
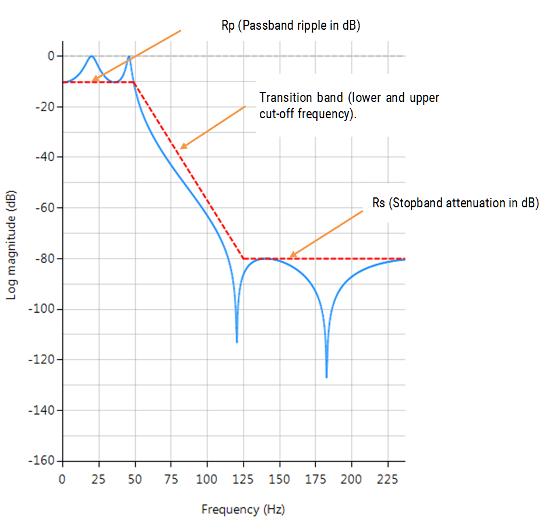
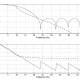
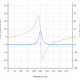
Vergleich der klassischen Entwurfsmethoden

Die unten gezeigten Frequenzgangdiagramme zeigen die Unterschiede zwischen den verschiedenen Prototyp-Entwurfsmethoden für ein Tiefpassfilter fünfter Ordnung mit den gleichen Spezifikationen. Wie zu sehen ist, rollt der Butterworth-Frequenzgang am langsamsten ab und der elliptische am schnellsten.

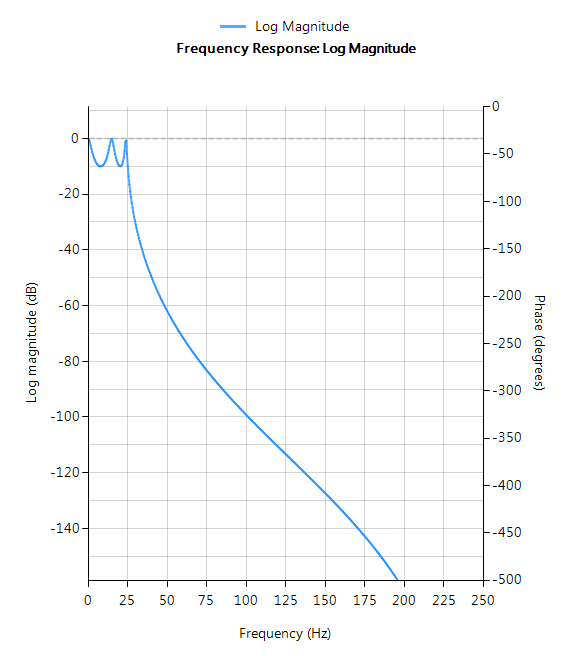
Elliptisch

Elliptische Filter bieten steilere Abrollcharakteristiken als Butterworth- oder Tschebyscheff-Filter, sind aber sowohl im Durchlass- als auch im Sperrbereich gleichschwebend. Im Allgemeinen erfüllen elliptische Filter die Entwurfsspezifikationen mit der niedrigsten Ordnung aller hier besprochenen Methoden.

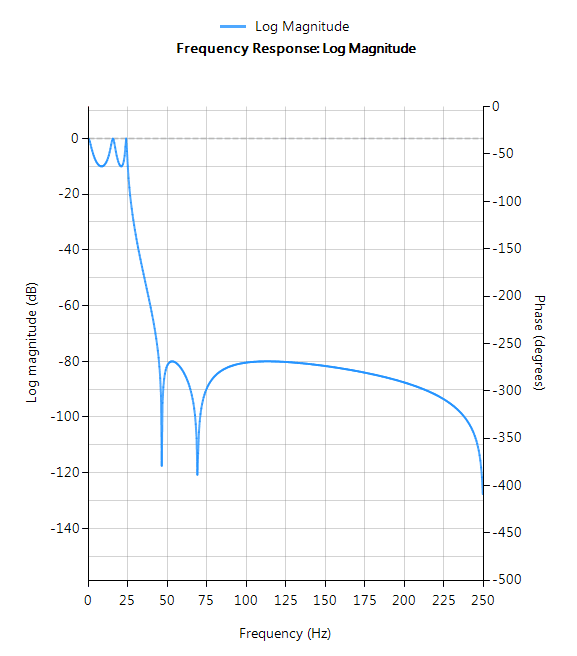
Filtereigenschaften

• Schnellster Roll-Off von allen unterstützten Prototypen
• Gleichwelligkeit sowohl im Durchlass- als auch im Sperrbereich
• Filter niedrigster Ordnung von allen unterstützten Prototypen
• Nichtlineare Durchlassband-Phaseneigenschaften
• Gute Wahl für Echtzeitsteuerung und Anwendungen mit hohem Durchsatz (RF-Anwendungen)

Butterworth

Butterworth-Filter haben einen maximal flachen Amplitudengang im Durchlassbereich und eine monotone Gesamtcharakteristik, was sie zu einer guten Wahl für DC- und Niederfrequenz-Messanwendungen macht, z. B. für Lastzellen. Diese höchst wünschenswerte “Glätte” wird jedoch mit einer geringeren Abflachung erkauft. Infolgedessen hat die Butterworth-Methode die langsamste Abrollcharakteristik aller hier besprochenen Methoden.

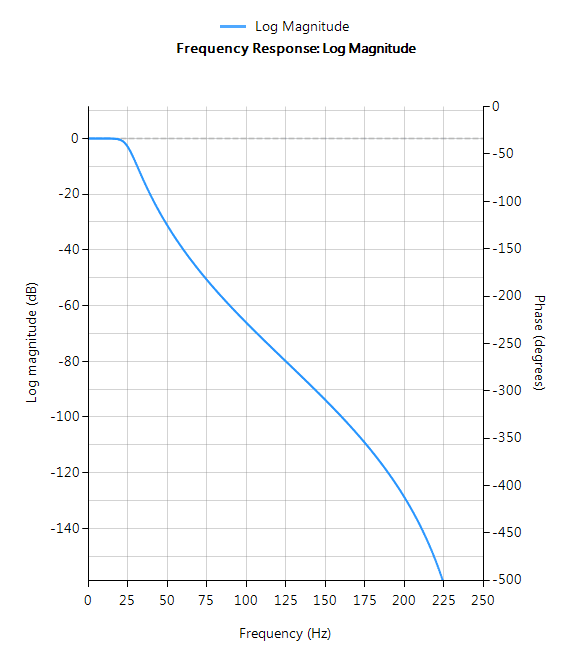
Filtereigenschaften

• Glatter monotoner Verlauf (keine Welligkeit)
• Langsamster Roll-Off für äquivalente Ordnung
• Höchste Ordnung von allen unterstützten Prototypen
• Linearerer Phasengang im Durchlassbereich als alle anderen Methoden
• Gute Wahl für DC-Messungen und Audioanwendungen

Tschebyscheff-Typ I

Tschebyscheff-Filter vom Typ I sind im Durchlassbereich äquirippel und im Sperrbereich monoton. Als solche rollen Typ-I-Filter schneller ab als Tschebyscheff-Typ-II- und Butterworth-Filter, allerdings auf Kosten einer größeren Durchlassbandwelligkeit.

Filtereigenschaften

• Durchlassband-Welligkeit
• Maximal flacher Sperrbereich
• Schnellerer Roll-Off als Butterworth und Tschebyscheff Typ II
• Guter Kompromiss zwischen Elliptic und Butterworth

Tschebyscheff-Typ II

Tschebyscheff-Filter vom Typ II sind monoton im Durchlassbereich und gleichwellig im Sperrbereich, was sie zu einer guten Wahl für Brückensensoranwendungen macht. Obwohl Filter, die mit der Typ-II-Methode entworfen wurden, langsamer abrollen als solche, die mit der Tschebyscheff-Typ-I-Methode entworfen wurden, ist der Roll-Off schneller als bei Filtern, die mit der Butterworth-Methode entworfen wurden.

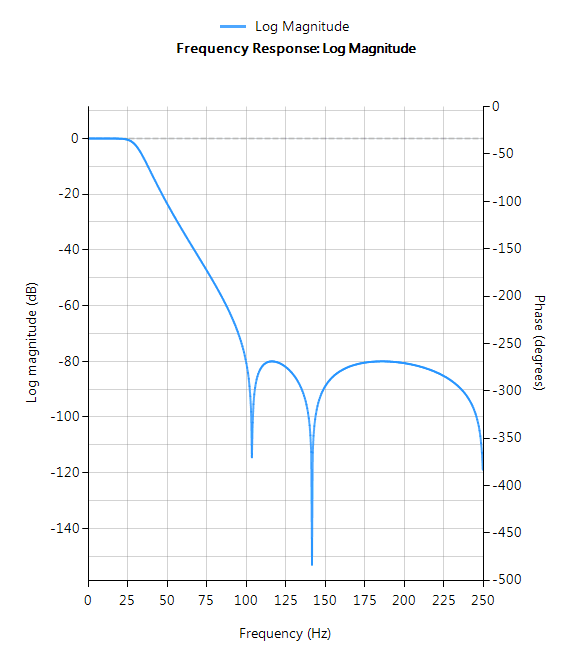
Filtereigenschaften

• Maximal flacher Durchlassbereich
• Schnellerer Roll-Off als Butterworth
• Langsamerer Roll-Off als Tschebyscheff Typ I
• Gute Wahl für DC-Messanwendungen

 

 

Demo herunterladen

Lizenzierung