Für viele IoT-Sensormessanwendungen ist ein IIR- oder FIR-Filter nur eine der vielen Komponenten, die für einen Algorithmus benötigt werden. Dabei kann es sich um einen Powerline Interference Canceller für eine biomedizinische Anwendung oder sogar um einen einfacheren DC-Wägezellenfilter handeln. In vielen Fällen ist es notwendig, einen Filter in einen vollständigen Algorithmus in einem anderen Bereich zu integrieren.
Matlab ist eine etablierte, von Mathworks entwickelte Sprache für numerische Berechnungen, die den Entwurf von Algorithmen, Matrixdatenmanipulationen und Datenanalysen ermöglicht. Das Produkt bietet eine breite Palette von Algorithmen und Unterstützungsfunktionen für Signalverarbeitungsanwendungen und ist daher bei vielen Wissenschaftlern und Ingenieuren weltweit sehr beliebt.
ASN Filter Designer automatischer Code-Generator für Matlab
Der ASN Filter Designer vereinfacht durch seinen automatischen Codegenerator den Export eines entworfenen Filters nach Matlab erheblich. Der Code-Generator unterstützt alle Aspekte des ASN Filter Designer, so dass ein komplettes Design, bestehend aus H1, H2 und H3 Filtern und mathematischen Operatoren, vollständig in einen Algorithmus in Matlab integriert werden kann.
Auf den Matlab-Codegenerator kann über die Filterzusammenfassungsoptionen zugegriffen werden (wie rechts dargestellt). Wenn Sie diese Option auswählen, wird automatisch eine Matlab .m-Datei auf der Grundlage des aktuellen Entwurfs erzeugt.
Eine bequeme Verknüpfung zu den relevanten Framework-Dateien und Beispielen ist in der Symbolleiste Filterzusammenfassung über das Ordnersymbol verfügbar (siehe links).
Mit Hilfe der drei Framework-Dateien können Sie eine Demo Ihrer Wahl auf der Grundlage der exportierten Filter-Spezifikationen erstellen. Das Framework unterstützt sowohl reelle als auch komplexe Filter nur in Fließkomma.
Framework-Dateien und Beispiele
Um den generierten Code in Matlab zu verwenden, ohne die Signal Processing Toolbox zu benötigen, werden die folgenden drei Framework-Dateien im Verzeichnis \Matlab des ASN Filter Designers bereitgestellt:
ASNFDMatlabFilterData.mASNFDMatlabImport.mASNFDFilter.m
Diese Framework-Dateien haben keine speziellen Matlab-Toolbox-Abhängigkeiten, und das Beispielskript ASNFDMatlabDemo.m demonstriert die Einfachheit, mit der das Framework in Ihre Anwendung für Ihren entworfenen Filter integriert werden kann. In ASNFDMatlabDemo.m sind mehrere Beispielfilter enthalten, die mit dem automatischen Codegenerator erzeugt wurden, damit Sie gleich loslegen können!
Vergleich der Ergebnisse mit Matlab’s Signal Processing Toolbox
Es ist manchmal aufschlussreich, die Ergebnisse der DSP-Bibliotheksfunktionen des ASN Filter Designers mit denen der Signal Processing Toolbox von Matlab zu vergleichen.
Entwurf eines IIR-Tschebyscheff-Filters vom Typ I mit den folgenden Spezifikationen:
| Fs: | 500Hz |
| Passband frequency: | 0-25Hz |
| Type: | Lowpass |
| Method: | Chebyshev Type I |
| Stopband attenuation @ 125Hz: | ≥ 80 dB |
| Passband ripple: | ≤ 0.1dB |
| Order: | 5 |
Durch die grafische Eingabe der Spezifikationen in den ASN Filter Designer und die Feinabstimmung der Designmarkerpositionen entwirft das Tool das Filter automatisch als Biquad-Kaskade. Beachten Sie, dass das Tool automatisch die erforderliche Filterordnung findet und im Wesentlichen automatisch die genaue technische Spezifikation des Filters erstellt!
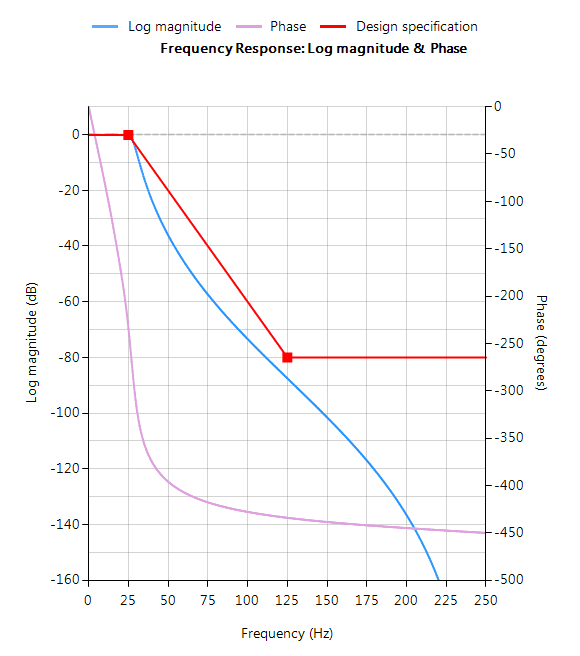
Der Frequenzgang eines IIR-Tschebyscheff-Tiefpassfilters 5. Ordnung, der den Spezifikationen entspricht, ist unten dargestellt:
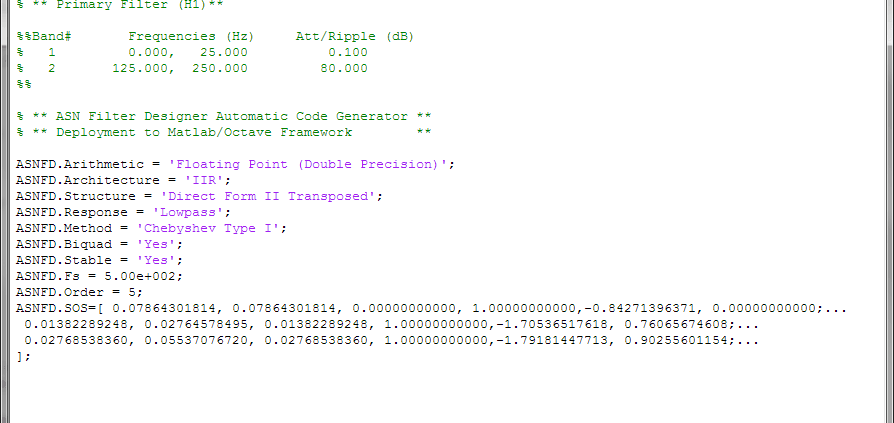
Die resultierenden Filterkoeffizienten sind:
Entwurf desselben Filters in Matlab mit der Signal Processing Toolbox:
Fs=500; Rp=0.1; Rs=80; F=2*[25,125]/Fs; [N,Wn]=cheb1ord(F(1),F(2),Rp,Rs) [z, p, k] = cheby1(N,Rp,Wn,'low'); % design lowpass [sos,g]=zp2sos(z,p,k,'up') % generate SOS form
Wenn wir das Skript ausführen, erhalten wir das folgende Ergebnis, wobei jede Zeile von sos ein Biquad ist, das wie folgt angeordnet ist: b0 b1 b2 a0 a1 a2
Analysiert man beide Koeffizientensätze im Zähler und im Nenner, erhält man genau das gleiche Ergebnis! Aber was ist mit der Verstärkung? Matlab gibt eine Nettoverstärkung aus, g = 3.0096e-05 , aber der ASN Filter Designer weist jedem Biquad eine optimale Verstärkung zu. Kombiniert man also die Verstärkungen der Biquad-Abschnitte, d.h. 0.078643, 0.013823 und 0.027685 , so ergibt sich eine Nettoverstärkung von 3.0096e-05, was genau der gleichen Nettoverstärkung wie in Matlab entspricht!
Fazit: Die Funktionen der DSP IIR Bibliothek des ASN Filter Designers entsprechen vollständig den Ergebnissen der Signal Processing Toolbox von Matlab!
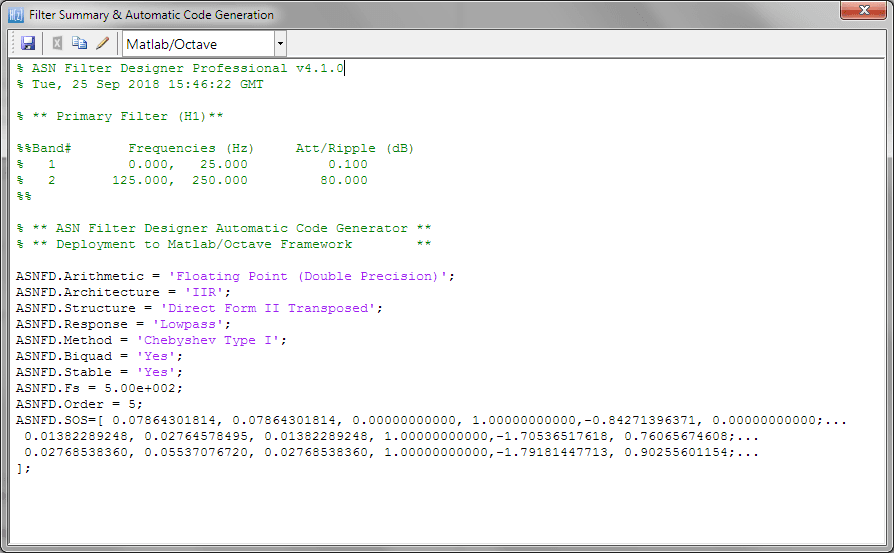
Der komplette automatisch generierte Code ist unten dargestellt, wo man sehen kann, dass die Biquad-Verstärkungen mit den Feedforward-Koeffizienten vormultipliziert wurden.
Verwendung des generierten Codes mit Signal Processing Toolbox
Wenn Sie Signal Processing Toolbox installiert haben, können Sie die in SOS generierten Koeffizienten direkt mit dem Befehl sosfilt()verwenden, z. B.
Clear all; ASNFD_SOS=[ 0.07864301814, 0.07864301814, 0.00000000000, 1.00000000000,-0.84271396371, 0.00000000000;... 0.01382289248, 0.02764578495, 0.01382289248, 1.00000000000,-1.70536517618, 0.76065674608;... 0.02768538360, 0.05537076720, 0.02768538360, 1.00000000000,-1.79181447713, 0.90255601154;... ]; y=sosfilt(ASNFD_SOS, x); % x is your input data plot(x,y); % plot results
Wie man sieht, ist es so einfach wie das Kopieren und Einfügen der Filterkoeffizienten aus der Filterübersicht des ASN Filter Designers in ein Matlab-Skript.




Leave a Reply
Want to join the discussion?Feel free to contribute!