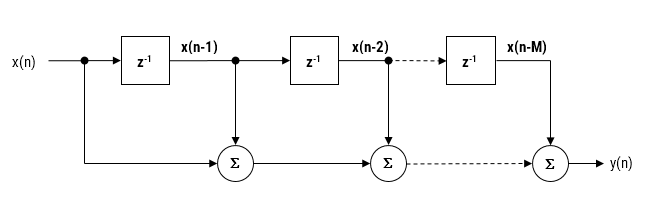
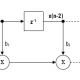
The moving average filter

The moving average (MA) filter is perhaps one of the most widely used FIR filters due to its conceptual simplicity and ease of implementation. As seen in the diagram below, notice that the filter doesn’t require any multiplications, just additions and a delay line, making it very suitable for many extreme low-power embedded devices with basic computational capabilities.

However, despite its simplicity, the moving average filter is optimal for reducing random noise while retaining a sharp step response, making it a versatile building block for smart sensor signal processing applications.

A moving average filter of length \(L\) for an input signal \(x(n)\) may be defined as follows:

\(y(n)=\large{\frac{1}{L}}\normalsize{\sum\limits_{k=0}^{L-1}x(n-k)}\) for \(\normalsize{n=0,1,2,3….}\)

Where, a simple rule of thumb states that the amount of noise reduction is equal to the square-root of the number of points in the average. For example, an MA of length 9 will result in a factor 3 noise reduction.

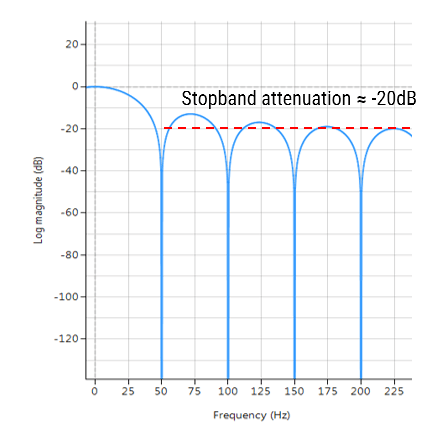Frequency response of an MA filter of length 9. Notice the poor stopband attentuation at around -20dB.

Advantages

Most commonly used digital lowpass filter.
Optimal for reducing random noise while retaining a sharp step response.
Good smoother (time domain).
Unity valued filter coefficients, no MAC (multiply and accumulate) operations required.
Conceptually simple to implement.

Disadvantages

Inflexible frequency response: nudging a conjugate zero pair results in non-unity coefficients.
Poor lowpass filter (frequency domain): slow roll-off and terrible stopband attenuation characteristics.

Implementation

The MA filter may be implemented in ASN FilterScript as follows:

ClearH1;  // clear primary filter from cascade
Main();
Hd=movaver(8,"symbolic");  // design an 8th order MA
Num = getnum(Hd);   // define numerator coefficients
Den = {1};          // define denominator coefficients
Gain = getgain(Hd); // define gain

A more computationally efficient implementation of the MA filter is discussed here.