FIR-Filter (finite impulse response) sind für viele sanwendungen von Signalverarbeitung nützlich, z.B. Audiosignalverarbeitung und Rauschunterdrückung.
Posts
What are Finite Impulse Respsonse (FIR) Filters? And how to design FIR Filters in ASN Filter Designer and which filters does ASN Filter Designer support?
DSP for engineers: the ASN Filter Designer is the ideal tool to analyze and filter the sensor data quickly. Create an algorithm within hours instead of days. When you are working with sensor data, you probably recognize these challenges:
- My sensor data signals are too weak to even make an analysis. So, strengthening of the signals is needed
- Where I would expect a flat line, the data looks like a mess because of interference and other containments. I need to clean the data first before analysis
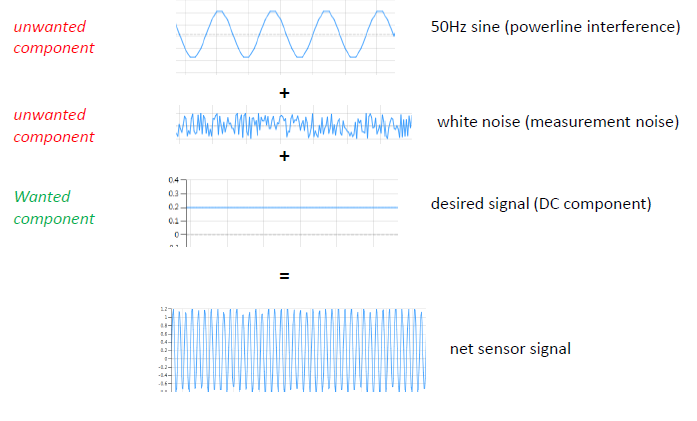
Until now, you’ve probably spent days or even weeks working on your signal analysis and filtering? The development trajectory is generally slow and very painful.
In fact, just think about the number of hours that you could have saved if you had design tool that managed all of the algorithmic details for you. ASN Filter Designer is an industry standard solution used by thousands of professional developers worldwide working on IoT projects.
Our close collaboration with Arm and ST ensures that all designed filters are 100% compatible with all Arm Cortex-M processors, such as ST’s popular STM32 family.

Challenges for engineers
- 90% of IoT smart sensors are based on Arm Cortex-M processor technology
- Sensor signal processing is difficult
- Sensors have trouble with all kinds of interference and undesirable components
- How do I design a filter that meets my requirements?
- How can I verify my designed filter on test data?
- Clean sensor data is required for better product performance
- Time consuming process to implement a filter on an embedded processor
- Time is money!
Designers hit a ‘brick wall’ with traditional tooling. Standard tooling requires an iterative, trial and error approach or expert knowledge. Using this approach, a considerable amount of valuable engineering time is wasted. ASN Filter Designer helps you with an interactive method of design, whereby the tool automatically enters the technical specifications based on the graphical user requirements.
Fast DSP algorithm development
- Fully validated filter design: suitable for deployment in DSP, micro-controller, FPGA, ASIC or PC application.
- Automatic detailed design documentation: expediting peer review and lowing project risks by helping the designer create a paper trail.
- Simple handover: project file, documentation and test results provide a painless route for handover to colleagues or other teams.
- Easily accommodate other scenarios in the future: Design may be simply modified in the future to accommodate other requirements and scenarios, such as 60Hz powerline interference cancellation, instead of the European 50Hz.
ASN Filter Designer: the fast and intuitive filter designer
The ASN Filter Designer is the ideal tool to analyze and filter the sensor data quickly. When needed, you can easily deploy your data for further analyze for tools such as Matlab and Python. As such it’s ideal for engineers who need and powerful signal analyser and need to create a data filter for their IoT application. Certainly, when you have to create data filtering once in a while. Compared to other tools, you can create an algorithm within hours instead of days.
Easily deploy your algorithms to Matlab, Python, C++ and Arm
A big timesaver of the ASN Filter Designer is that you can easily deploy your algorithms to Matlab, Python, C++ or directly on an Arm microcontroller with the automatic code generators.
Instant pain relief
Just think about the number of hours that you could have saved if you had design tool that managed all of the algorithmic details for you.
ASN Filter Designer is an industry standard solution used by thousands of professional developers worldwide working on IoT projects. Our close collaboration with Arm and ST ensures that the all filters are 100% compatible with all Arm Cortex-M processors.
How much pain relief can 125 Euro buy you?
Because a lot of engineers need our ASN Filter Designer for a short time, a 125 Euro license for just 3 months is possible!
Just ask yourself: is 125 Euro a fair price to pay for instant pain relief and results? We think so. Besides, we have a license for 1 year and even a perpetual license. Download the demo to see for yourself or contact us for more information.
Finite impulse response (FIR) filters are useful for a variety of sensor signal processing applications, including audio and biomedical signal processing. Although several practical implementations for the FIR exist, the Direct Form Transposed structure offers the best numerical accuracy for floating point implementation. However, when considering fixed point implementation on a micro-controller, the Direct Form structure is considered to be the best choice by virtue of its large accumulator that accommodates any intermediate overflows.
This application note specifically addresses FIR filter design and implementation on a Cortex-M based microcontroller with the ASN Filter Designer for both floating point and fixed point applications via the Arm CMSIS-DSP software framework. Details are also given (including an Arm reference software pack) regarding implementation of the FIR filter in Arm/Keil’s MDK industry standard Cortex-M micro-controller development kit.
Introduction
ASN Filter Designer provides engineers with a powerful DSP experimentation platform, allowing for the design, experimentation and deployment of complex FIR digital filter designs for a variety of sensor measurement applications. The tool’s advanced functionality, includes a graphical based real-time filter designer, multiple filter blocks, various mathematical I/O blocks, live symbolic math scripting and real-time signal analysis (via a built-in signal analyser). These advantages coupled with automatic documentation and code generation functionality allow engineers to design and validate a digital filter within minutes rather than hours.
The Arm CMSIS-DSP (Cortex Microcontroller Software Interface Standard) software framework is a rich collection of over sixty DSP functions (including various mathematical functions, such as sine and cosine; IIR/FIR filtering functions, complex math functions, and data types) developed by Arm that have been optimised for their range of Cortex-M processor cores.

The framework makes extensive use of highly optimised SIMD (single instruction, multiple data) instructions, that perform multiple identical operations in a single cycle instruction. The SIMD instructions (if supported by the core) coupled together with other optimisations allow engineers to produce highly optimised signal processing applications for Cortex-M based micro-controllers quickly and simply.
ASN Filter Designer fully supports the CMSIS-DSP software framework, by automatically producing optimised C code based on the framework’s DSP functions via its code generation engine.
Designing FIR filters with the ASN Filter Designer
ASN Filter Designer provides engineers with an easy to use, intuitive graphical design development platform for FIR digital filter design. The tool’s real-time design paradigm makes use of graphical design markers, allowing designers to simply draw and modify their magnitude frequency response requirements in real-time while allowing the tool automatically fill in the exact specifications for them.
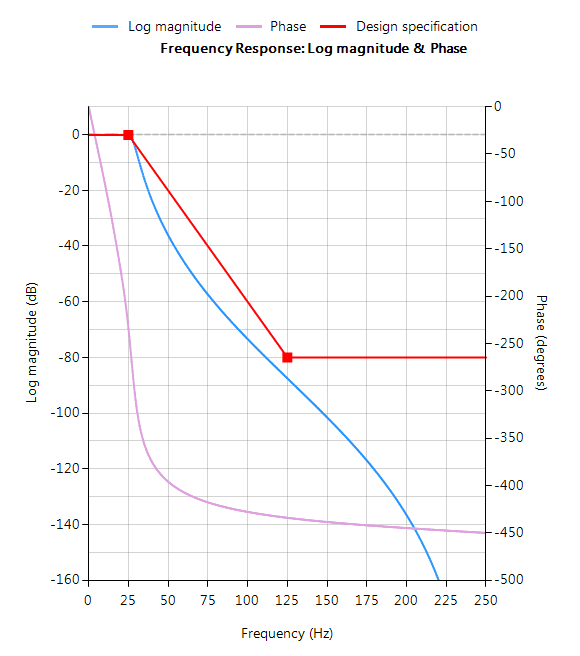
Consider the design of the following technical specification:
| Fs: | 500Hz |
| Passband frequency: | 0-25Hz |
| Type: | Lowpass |
| Method: | Parks-McClellan |
| Stopband attenuation @ 125Hz: | ≥ 80 dB |
| Passband ripple: | < 0.01dB |
| Order: | Small as possible |
Graphically entering the specifications into the ASN Filter Designer, and fine tuning the design marker positions, the tool automatically designs the filter), automatically choosing the required filter order, and in essence – automatically producing the filter’s exact technical specification!
The frequency response of a filter meeting the specification is shown below:
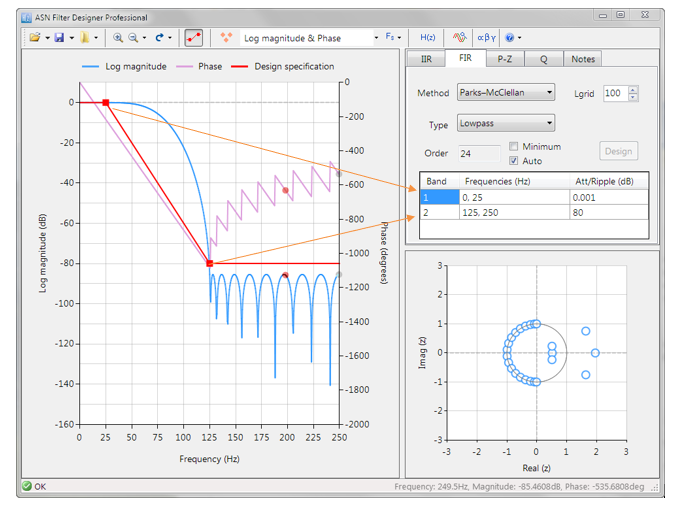
This Lowpass filter will form the basis of the discussion presented herein.
Parks–McClellan algorithm
The Parks–McClellan algorithm is an iterative algorithm for finding the optimal Chebyshev FIR filter. The algorithm uses an indirect method for finding the optimal filter coefficients, that offers a degree of flexibility over other FIR design methods, in that each band may be individually customised in order to suit the designer’s requirements.
The primary FIR filter designer UI implements the Parks-McClellan algorithm, allowing for the design of the following filter types:
| Filter Types | Description |
| Lowpass | Designs a lowpass filter. |
| Highpass | Designs a highpass filter. |
| Bandpass | Designs a bandpass filter. |
| Bandstop | Designs a bandstop filter. |
| Multiband | Designs a multiband filter with an arbitrary frequency response. |
| Hilbert transformer | Designs an all-pass filter with a -90 degree phase shift. |
| Differentiator | Designs a filter with +20dB/decade slope and +90 degree phase shift. |
| Double Differentiator | Designs a filter with +40dB/decade slope and a +90 degree phase shift. |
| Integrator | Designs a filter with -20dB/decade slope and a -90 degree phase shift. |
| Double Integrator | Designs a filter with -40dB/decade slope and a -90 degree phase shift. |
These ten filter types provide designers with a great deal of flexibility for a variety of IoT applications. Design requirements may be simply specified via the use of the design markers. In all cases, the tool will automatically calculate the required filter order to meet the designer’s specification.

The Parks-McClellan algorithm is an optimal Chebyshev FIR design method. However, the algorithm may not converge for some specifications. In such cases, increasing the distance between the design marker bands generally helps.
Other FIR design methods
Designers looking to experiment with other types of FIR design methods may use the ASN FilterScript live symbolic math scripting language. The scripting language supports over 65 scientific commands and provides designers with a familiar and powerful programming language, while at the same time allowing them to implement complex symbolic mathematical expressions. The following functions are supported:
| Function | Description |
| movaver | Moving average FIR filter design. |
| firwin | FIR filter design based on the Window method. |
| firarb | Designs an FIR Window based filter with an arbitrary magnitude response. |
| firkaiser | Designs an FIR filter based on the Kaiser window method. |
| firgauss | Designs an FIR Gaussian lowpass filter. |
| savgolay | Design an FIR Savitzky-Golay lowpass smoothing filter. |
Please refer to the ASN FilterScript reference guide for more details.
All filters designed in ASN FilterScript are designed using double precision arithmetic in the H2 filter sandbox. An H2 filter must be transformed to an H1 (primary) filter for deployment.
This may be simply achieved via the P-Z options menu:
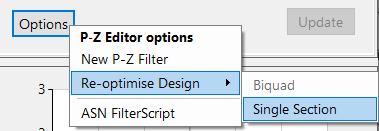
The re-optimise method automatically analyses and converts the H2 filter into an H1 filter.
Floating point implementation
When implementing a filter in floating point (i.e. using double or single precision arithmetic) the Direct Form Transposed structure is considered the most numerically accurate. This can be readily seen by analysing the difference equations below (used for implementation), as the undesirable effects of numerical swamping are minimised, since floating point addition is performed on numbers of similar magnitude.
\(\displaystyle \begin{eqnarray}y(n) & = &b_0x(n) &+& w_1(n-1) \\ w_1(n)&=&b_1x(n) &+& w_2(n-1) \\ w_2(n)&=&b_2x(n) &+& w_3(n-1) \\ \vdots\quad &=& \quad\vdots &+&\quad\vdots \\ w_q(n)&=&b_qx(n) \end{eqnarray}\)
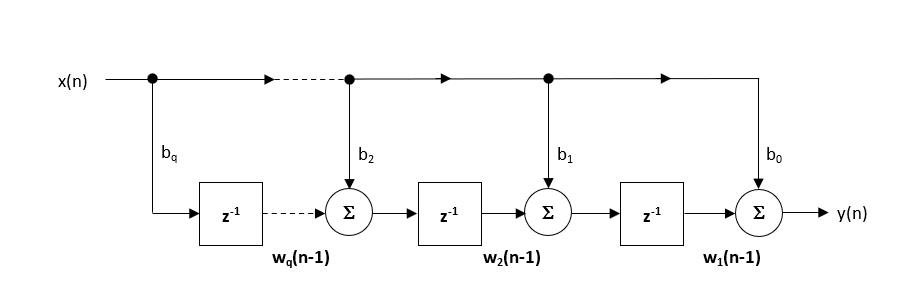
\(\displaystyle \begin{eqnarray}y(n) & = &b_0x(n) &+& w_1(n-1) \\ w_1(n)&=&b_1x(n) &+& w_2(n-1) \\ w_2(n)&=&b_2x(n) &+& w_3(n-1) \\ \vdots\quad &=& \quad\vdots &+&\quad\vdots \\ w_q(n)&=&b_qx(n) \end{eqnarray}\)
The quantisation and filter structure settings used to implement the FIR can be found under the Q tab (as shown below).

Despite the Direct Form Transposed structure being the most efficient for floating point implementation, the Arm CMSIS-DSP library does not currently support the Direct Form Transposed structure for FIR filters. Only the Direct Form structure is supported.
Setting Arithmetic to Single Precision and Structure to Direct Form and clicking on the Apply button configures the FIR considered herein for the CMSIS-DSP software framework.
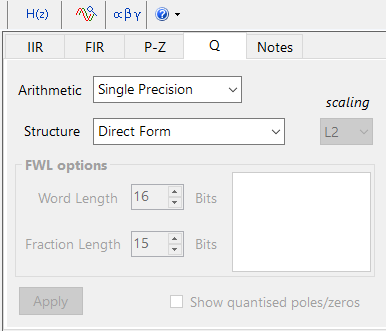

The optimised functions within the Arm CMSIS-DSP framework currently support Single Precision arithmetic only.
Support for Double Precision and the Direct Form Transposed structure will be added in future releases.
Fixed point implementation
When implementing a filter with fixed point arithmetic, the Direct Form structure is considered to be the best choice by virtue of its large accumulator that accommodates any intermediate overflows. The Direct Form structure and associated difference equation are shown below.
\(\displaystyle y(n) = b_0x(n) + b_1x(n-1) + b_2x(n-2) + …. +b_qx(n-q) \)
The CMSIS-DSP Framework supports Q7, Q15 and Q31 coefficient quantisation only. The options may be simply specified via the quantisation tab Q as shown below:
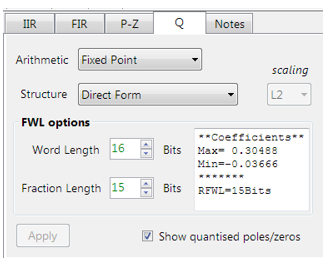
The tool’s inbuilt analytics (shown in the textbox) are intended to help the designer choose the most suitable quantisation settings.
As seen on the left, the tool has recommended a RFWL (recommended fraction length) of 15bits (Q15) for the coefficients, which is as required.
The Direct form structure is chosen over the Direct Form Transposed as a single (40-bit) accumulator can be used. The tool’s automatic code generator makes use of CMSIS-DSP’s 64-bit accumulators functions, so that the final C code deployed to a Cortex-M device will not overflow.
Deploying Arm CMSIS-DSP compliant code
The ASN Filter Designer’s automatic code generation engine facilitates the export of a designed filter to Cortex-M Arm based processors via the Arm CMSIS-DSP software framework. The tool’s built-in analytics and help functions assist the designer in successfully configuring the design for deployment.
Select the Arm CMSIS-DSP framework from the selection box in the filter summary window:
The automatically generated C code based on the Arm CMSIS-DSP framework for direct implementation on an Arm based Cortex-M processor is shown below:
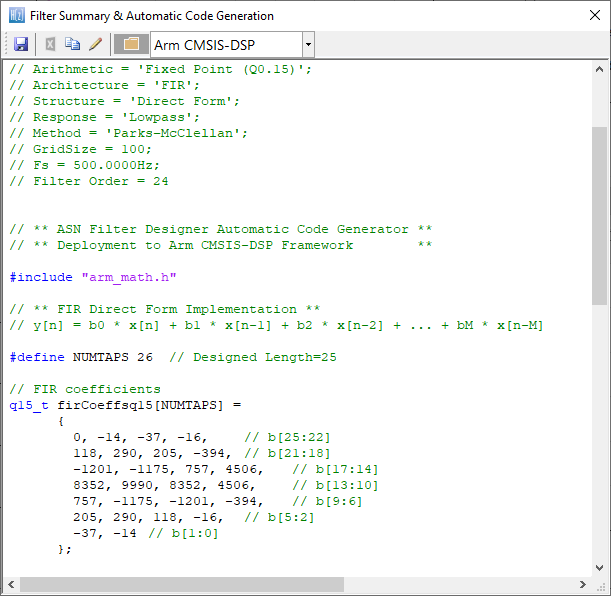
This code may be directly used in any Cortex-M based development project.
Arm Keil’s MDK (uVision)
As mentioned above, the code generated by the Arm CMSIS DSP code generator may be directly used in any Cortex-M based development project tooling, such as Arm Keil’s industry standard uVision MDK (micro-controller development kit).
The following Arm software pack is available on Keil’s website for using this code directly with Keil uVision MDK.
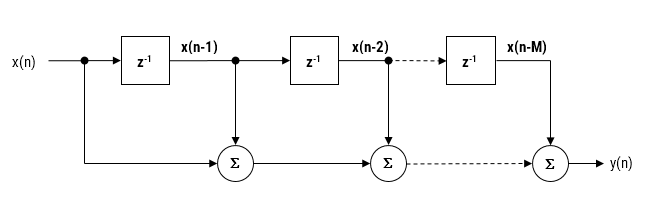
As discussed in a previous article, the moving average (MA) filter is perhaps one of the most widely used digital filters due to its conceptual simplicity and ease of implementation. The realisation diagram shown below, illustrates that an MA filter can be implemented as a simple FIR filter, just requiring additions and a delay line.
Modelling the above, we see that a moving average filter of length \(\small\textstyle L\) for an input signal \(\small\textstyle x(n)\) may be defined as follows:
\( y(n)=\large{\frac{1}{L}}\normalsize{\sum\limits_{k=0}^{L-1}x(n-k)}\quad \text{for} \quad\normalsize{n=0,1,2,3….}\label{FIRdef}\tag{1}\)
This computation requires \(\small\textstyle L-1\) additions, which may become computationally demanding for very low power processors when \(\small\textstyle L\) is large. Therefore, applying some lateral thinking to the computational challenge, we see that a much more computationally efficient filter can be used in order to achieve the same result, namely:
\(H(z)=\displaystyle\frac{1}{L}\frac{1-z^{-L}}{1-z^{-1}}\tag{2}\label{TF}\)
with the difference equation,
\(y(n) =y(n-1)+\displaystyle\frac{x(n)-x(n-L)}{L}\tag{3}\)
Notice that this implementation only requires one addition and one subtraction for any value of \(\small\textstyle L\). A further simplification (valid for both implementations) can be achieved in a pre-processing step prior to implementing the difference equation, i.e. scaling all input values by \(\small\textstyle L\). If \(\small\textstyle L\) is a power of two (e.g. 4,8,16,32..), this can be achieved by a simple binary shift right operation.
Is it an IIR or actually an FIR?
Upon initial inspection of the transfer function of Eqn. \(\small\textstyle\eqref{TF}\), it appears that the efficient Moving average filter is an IIR filter. However, analysing the pole-zero plot of the filter (shown on the right for \(\small\textstyle L=8\)), we see that the pole at DC has been cancelled by a zero, and that the resulting filter is actually an FIR filter, with the same result as Eqn. \(\small\textstyle\eqref{FIRdef}\).
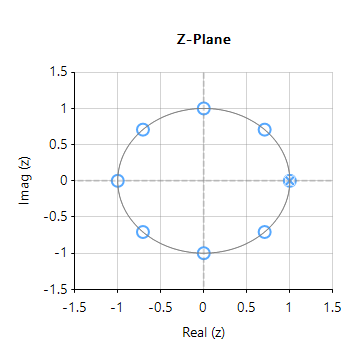
Notice also that the frequency spacing of the zeros (corresponding to the nulls in the frequency response) are at spaced at \(\small\textstyle\pm\frac{Fs}{L}\). This can be readily seen for this example, where an MA of length 8, sampled at \(\small\textstyle 500Hz\), results in a \(\small\textstyle\pm62.5Hz\) resolution.
As a final point, notice that the our efficient filter requires a delay line of length \(\small\textstyle L+1\), compared with the FIR delay line of length, \(\small\textstyle L\). However, this is a small price to pay for the computation advantage of a filter just requiring one addition and one subtraction. As such, the MA filter of Eqn. \(\small\textstyle\eqref{TF}\) presented herein is very attractive for very low power processors, such as the Arm Cortex-M0 that have been traditionally overlooked for DSP operations.
Implementation
The MA filter of Eqn. \(\small\textstyle\eqref{TF}\) may be implemented in ASN FilterScript as follows:
ClearH1; // clear primary filter from cascade
interface L = {2,32,2,4}; // interface variable definition
Main()
Num = {1,zeros(L-1),-1}; // define numerator coefficients
Den = {1,-1}; // define denominator coefficients
Gain = 1/L; // define gain
A digital filter is a mathematical algorithm that operates on a digital dataset (e.g. sensor data) in order extract information of interest and remove any unwanted information. Applications of this type of technology, include removing glitches from sensor data or even cleaning up noise on a measured signal for easier data analysis. But how do we choose the best type of digital filter for our application? And what are the differences between an IIR filter and an FIR filter?
Digital filters are divided into the following two categories:
- Infinite impulse response (IIR)
- Finite impulse response (FIR)
As the names suggest, each type of filter is categorised by the length of its impulse response. However, before beginning with a detailed mathematical analysis, it is prudent to appreciate the differences in performance and characteristics of each type of filter.
Example
In order to illustrate the differences between an IIR and FIR, the frequency response of a 14th order FIR (solid line), and a 4th order Chebyshev Type I IIR (dashed line) is shown below in Figure 1. Notice that although the magnitude spectra have a similar degree of attenuation, the phase spectrum of the IIR filter is non-linear in the passband (\(\small 0\rightarrow7.5Hz\)), and becomes very non-linear at the cut-off frequency, \(\small f_c=7.5Hz\). Also notice that the FIR requires a higher number of coefficients (15 vs the IIR’s 10) to match the attenuation characteristics of the IIR.
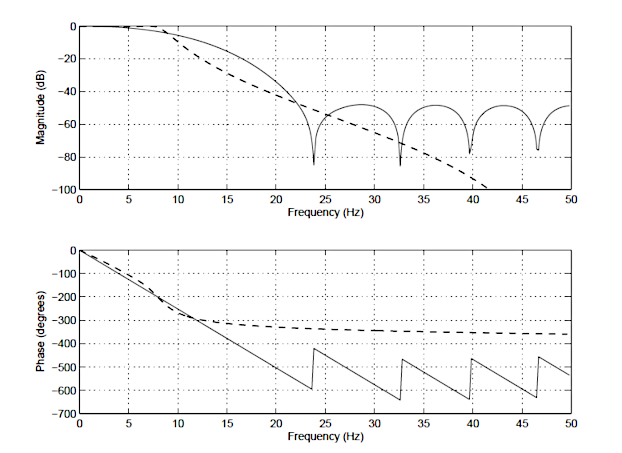
These are just some of the differences between the two types of filters. A detailed summary of the main advantages and disadvantages of each type of filter will now follow.
IIR filters
IIR (infinite impulse response) filters are generally chosen for applications where linear phase is not too important and memory is limited. They have been widely deployed in audio equalisation, biomedical sensor signal processing, IoT/IIoT smart sensors and high-speed telecommunication/RF applications.
Advantages
- Low implementation cost: requires less coefficients and memory than FIR filters in order to satisfy a similar set of specifications, i.e., cut-off frequency and stopband attenuation.
- Low latency: suitable for real-time control and very high-speed RF applications by virtue of the low number of coefficients.
- Analog equivalent: May be used for mimicking the characteristics of analog filters using s-z plane mapping transforms.
Disadvantages
- Non-linear phase characteristics: The phase charactersitics of an IIR filter are generally nonlinear, especially near the cut-off frequencies. All-pass equalisation filters can be used in order to improve the passband phase characteristics.
- More detailed analysis: Requires more scaling and numeric overflow analysis when implemented in fixed point. The Direct form II filter structure is especially sensitive to the effects of quantisation, and requires special care during the design phase.
- Numerical stability: Less numerically stable than their FIR (finite impulse response) counterparts, due to the feedback paths.
FIR filters
FIR (finite impulse response) filters are generally chosen for applications where linear phase is important and a decent amount of memory and computational performance are available. They have a widely deployed in audio and biomedical signal enhancement applications. Their all-zero structure (discussed below) ensures that they never become unstable for any type of input signal, which gives them a distinct advantage over the IIR.
Advantages
- Linear phase: FIRs can be easily designed to have linear phase. This means that no phase distortion is introduced into the signal to be filtered, as all frequencies are shifted in time by the same amount – thus maintaining their relative harmonic relationships (i.e. constant group and phase delay). This is certainly not case with IIR filters, that have a non-linear phase characteristic.
- Stability: As FIRs do not use previous output values to compute their present output, i.e. they have no feedback, they can never become unstable for any type of input signal, which is gives them a distinct advantage over IIR filters.
- Arbitrary frequency response: The Parks-McClellan and ASN FilterScript’s firarb() function allow for the design of an FIR with an arbitrary magnitude response. This means that an FIR can be customised more easily than an IIR.
- Fixed point performance: the effects of quantisation are less severe than that of an IIR.
Disadvantages
- High computational and memory requirement: FIRs usually require many more coefficients for achieving a sharp cut-off than their IIR counterparts. The consequence of this is that they require much more memory and significantly a higher amount of MAC (multiple and accumulate) operations. However, modern microcontroller architectures based on the Arm’s Cortex-M cores now include DSP hardware support via SIMD (signal instruction, multiple data) that expedite the filtering operation significantly.
- Higher latency: the higher number of coefficients, means that in general a linear phase FIR is less suitable than an IIR for fast high throughput applications. This becomes problematic for real-time closed-loop control applications, where a linear phase FIR filter may have too much group delay to achieve loop stability.
- Minimum phase filters: A solution to ovecome the inherent N/2 latency (group delay) in a linear filter is to use a so-called minimum phase filter, whereby any zeros outside of the unit circle are moved to their conjugate reciprocal locations inside the unit circle. The result of the zero flipping operation is that the magnitude spectrum will be identical to the original filter, and the phase will be nonlinear, but most importantly the latency will be reduced from N/2 to something much smaller (although non-constant), making it suitable for real-time control applications.
For applications where phase is less important, this may sound ideal, but the difficulty arises in the numerical accuracy of the root-finding algorithm when dealing with large polynomials. Therefore, orders of 50 or 60 should be considered a maximum when using this approach. Although other methods do exist (e.g. the Complex Cepstrum), transforming higher-order linear phase FIRs to their minimum phase cousins remains a challenging task. - No analog equivalent: using the Bilinear, matched z-transform (s-z mapping), an analog filter can be easily be transformed into an equivalent IIR filter. However, this is not possible for an FIR as it has no analog equivalent.
Mathematical definitions
As discussed in the introduction, the name IIR and FIR originate from the mathematical definitions of each type of filter, i.e. an IIR filter is categorised by its theoretically infinite impulse response,
y(n)=\sum_{k=0}^{\infty}h(k)x(n-k)
\)
and an FIR categorised by its finite impulse response,
y(n)=\sum_{k=0}^{N-1}h(k)x(n-k)
\)
We will now analyse the mathematical properties of each type of filter in turn.
IIR definition
As seen above, an IIR filter is categorised by its theoretically infinite impulse response,
\(\displaystyle y(n)=\sum_{k=0}^{\infty}h(k)x(n-k) \)
Practically speaking, it is not possible to compute the output of an IIR using this equation. Therefore, the equation may be re-written in terms of a finite number of poles \(\small p\) and zeros \(\small q\), as defined by the linear constant coefficient difference equation given by:
y(n)=\sum_{k=0}^{q}b_k x(n-k)-\sum_{k=1}^{p}a_ky(n-k)
\)
where, \(\small a_k\) and \(\small b_k\) are the filter’s denominator and numerator polynomial coefficients, who’s roots are equal to the filter’s poles and zeros respectively. Thus, a relationship between the difference equation and the z-transform (transfer function) may therefore be defined by using the z-transform delay property such that,
\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)\quad\stackrel{\displaystyle\mathcal{Z}}{\longleftrightarrow}\quad\frac{\sum\limits_{k=0}^q b_kz^{-k}}{1+\sum\limits_{k=1}^p a_kz^{-k}}
\)
As seen, the transfer function is a frequency domain representation of the filter. Notice also that the poles act on the output data, and the zeros on the input data. Since the poles act on the output data, and affect stability, it is essential that their radii remain inside the unit circle (i.e. <1) for BIBO (bounded input, bounded output) stability. The radii of the zeros are less critical, as they do not affect filter stability. This is the primary reason why all-zero FIR (finite impulse response) filters are always stable.
BIBO stability
A linear time invariant (LTI) system (such as a digital filter) is said to be bounded input, bounded output stable, or BIBO stable, if every bounded input gives rise to a bounded output, as
\(\displaystyle \sum_{k=0}^{\infty}\left|h(k)\right|<\infty \)
Where, \(\small h(k)\) is the LTI system’s impulse response. Analyzing this equation, it should be clear that the BIBO stability criterion will only be satisfied if the system’s poles lie inside the unit circle, since the system’s ROC (region of convergence) must include the unit circle. Consequently, it is sufficient to say that a bounded input signal will always produce a bounded output signal if all the poles lie inside the unit circle.
The zeros on the other hand, are not constrained by this requirement, and as a consequence may lie anywhere on z-plane, since they do not directly affect system stability. Therefore, a system stability analysis may be undertaken by firstly calculating the roots of the transfer function (i.e., roots of the numerator and denominator polynomials) and then plotting the corresponding poles and zeros upon the z-plane.
An interesting situation arises if any poles lie on the unit circle, since the system is said to be marginally stable, as it is neither stable or unstable. Although marginally stable systems are not BIBO stable, they have been exploited by digital oscillator designers, since their impulse response provides a simple method of generating sine waves, which have proved to be invaluable in the field of telecommunications.
Biquad IIR filters
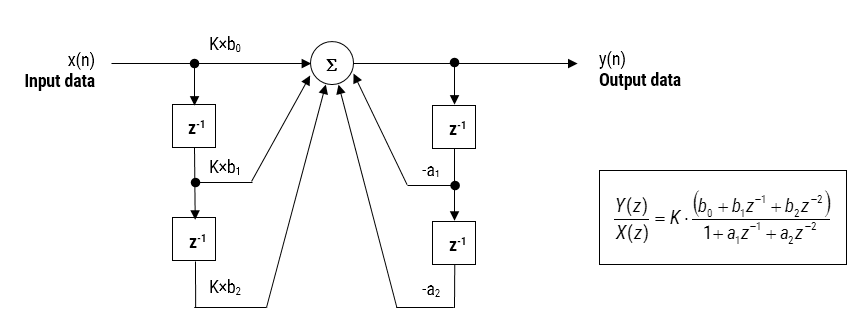
The IIR filter implementation discussed herein is said to be biquad, since it has two poles and two zeros as illustrated below in Figure 2. The biquad implementation is particularly useful for fixed point implementations, as the effects of quantization and numerical stability are minimised. However, the overall success of any biquad implementation is dependent upon the available number precision, which must be sufficient enough in order to ensure that the quantised poles are always inside the unit circle.
Figure 2: Direct Form I (biquad) IIR filter realization and transfer function.
Analysing Figure 2, it can be seen that the biquad structure is actually comprised of two feedback paths (scaled by \(\small a_1\) and \(\small a_2\)), three feed forward paths (scaled by \(\small b_0, b_1\) and \(\small b_2\)) and a section gain, \(\small K\). Thus, the filtering operation of Figure 1 can be summarised by the following simple recursive equation:
\(\displaystyle y(n)=K\times\Big[b_0 x(n) + b_1 x(n-1) + b_2 x(n-2)\Big] – a_1 y(n-1)-a_2 y(n-2)\)
Analysing the equation, notice that the biquad implementation only requires four additions (requiring only one accumulator) and five multiplications, which can be easily accommodated on any Cortex-M microcontroller. The section gain, \(\small K\) may also be pre-multiplied with the forward path coefficients before implementation.
A collection of Biquad filters is referred to as a Biquad Cascade, as illustrated below.
The ASN Filter Designer can design and implement a cascade of up to 50 biquads (Professional edition only).
Floating point implementation
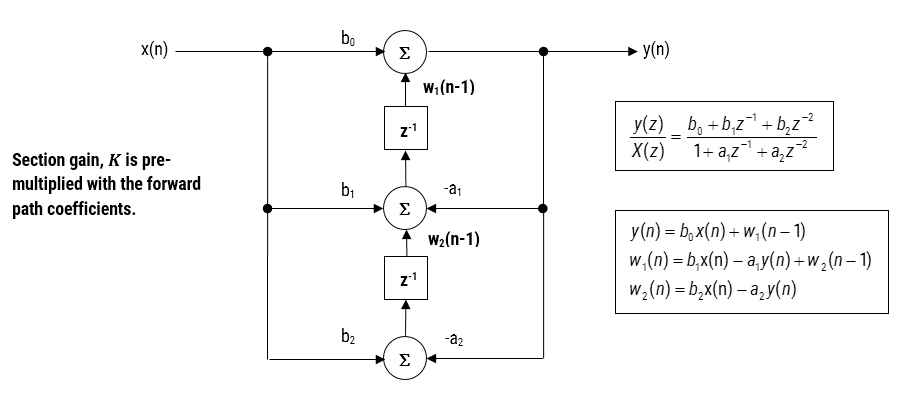
When implementing a filter in floating point (i.e. using double or single precision arithmetic) Direct Form II structures are considered to be a better choice than the Direct Form I structure. The Direct Form II Transposed structure is considered the most numerically accurate for floating point implementation, as the undesirable effects of numerical swamping are minimised as seen by analysing the difference equations.
Figure 3 – Direct Form II Transposed strucutre, transfer function and difference equations
The filter summary (shown in Figure 4) provides the designer with a detailed overview of the designed filter, including a detailed summary of the technical specifications and the filter coefficients, which presents a quick and simple route to documenting your design.
The ASN Filter Designer supports the design and implementation of both single section and Biquad (default setting) IIR filters.
FIR definition
Returning the IIR’s linear constant coefficient difference equation, i.e.
y(n)=\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)
\)
Notice that when we set the \(\small a_k\) coefficients (i.e. the feedback) to zero, the definition reduces to our original the FIR filter definition, meaning that the FIR computation is just based on past and present inputs values, namely:
y(n)=\sum_{k=0}^{q}b_kx(n-k)
\)
Implementation
Although several practical implementations for FIRs exist, the direct form structure and its transposed cousin are perhaps the most commonly used, and as such, all designed filter coefficients are intended for implementation in a Direct form structure.
The Direct form structure and associated difference equation are shown below. The Direct Form is advocated for fixed point implementation by virtue of the single accumulator concept.
\(\displaystyle y(n) = b_0x(n) + b_1x(n-1) + b_2x(n-2) + …. +b_qx(n-q) \)

The recommended (default) structure within the ASN Filter Designer is the Direct Form Transposed structure, as this offers superior numerical accuracy when using floating point arithmetic. This can be readily seen by analysing the difference equations below (used for implementation), as the undesirable effects of numerical swamping are minimised, since floating point addition is performed on numbers of similar magnitude.
\(\displaystyle \begin{eqnarray}y(n) & = &b_0x(n) &+& w_1(n-1) \\ w_1(n)&=&b_1x(n) &+& w_2(n-1) \\ w_2(n)&=&b_2x(n) &+& w_3(n-1) \\ \vdots\quad &=& \quad\vdots &+&\quad\vdots \\ w_q(n)&=&b_qx(n) \end{eqnarray}\)

Implementing your filter on an Arm Cortex-M processor
Although a few processor technologies exist for microcontrollers (e.g. RISC-V, Xtensa, MIPS), over 90% of the microcontrollers used in the smart product market are powered by so-called Arm Cortex-M processors that offer a combination of high algorithmic performance, low-power and security. The Arm Cortex-M4 is a very popular choice with several silicon vendors (including ST, TI, NXP, ADI, Nordic, Microchip, Renesas), as it offers DSP (digital signal processing) functionality traditionally found in more expensive devices and is low-power.
Filtering libraries and support
Arm and ASN provide developers with extensive easy-to-use tooling and tried and tested software libraries used internationally by tens of thousands of developers.
The Arm CMSIS-DSP software framework is interesting as it provides IoT developers with a rich collection of fast mathematical and vector functions, interpolation functions, digital filtering (FIR/IIR) and adaptive filtering (LMS) functions, motor control functions (e.g. PID controller), complex math functions and supports various data types, including fixed and floating point. The important point to make here is that all of these functions have been optimised for Arm Cortex-M processors, allowing you to focus on your application rather than worrying about optimisation.
Despite the broad functionality, the CMSIS-DSP library is somewhat limited for filters, so the flexible ASN DSP filtering library can be used instead, which supports the higher numerical accuracy Direct Form Transposed FIR filter structure and single section IIR filters. A benchmark of ASN’s floating point application-specific DSP filtering library versus Arm’s CMSIS-DSP library is shown below for three types of Arm cores.
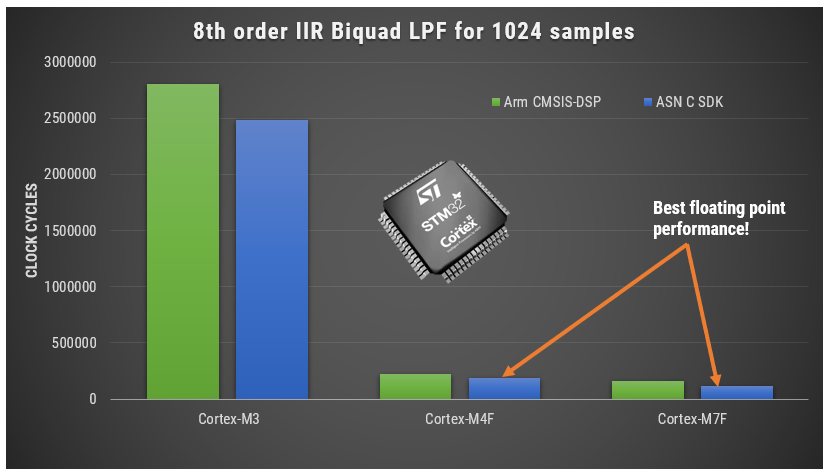
As seen, the performance of the ASN library is slightly faster by virtue of the application-specific nature of the implementation. The C code is automatically generated from the ASN Filter Designer tool.
What have we learned?
Digital filters are divided into the following two categories:
- Infinite impulse response (IIR)
- Finite impulse response (FIR)
IIR (infinite impulse response) filters are generally chosen for applications where linear phase is not too important and memory is limited. They have been widely deployed in audio equalisation, biomedical sensor signal processing, IoT/AIoT smart sensors and high-speed telecommunication/RF applications.
FIR (finite impulse response) filters are generally chosen for applications where linear phase is important and a decent amount of memory and computational performance are available. They have a widely deployed in audio and biomedical signal enhancement applications.
ASN Filter Designer provides engineers with everything they need to design, experiment and deploy complex IIR and FIR digital filters for a variety of IoT sensor measurement applications. These advantages coupled with automatic C code generation with ASN’s DSP filtering library functionality allow engineers to design, validate and then deploy their designs to an Arm Cortex-M processor within hours rather than more traditional routes that could take days.
Author
-

Sanjeev is a RTEI (Real-Time Edge Intelligence) visionary and expert in signals and systems with a track record of successfully developing over 26 commercial products. He is a Distinguished Arm Ambassador and advises top international blue chip companies on their AIoT/RTEI solutions and strategies for I5.0, telemedicine, smart healthcare, smart grids and smart buildings.
View all posts
6 reasons why ASN Filter Designer is a powerful real-time DSP platform e.g. life math scripting, tool creates your technical specification and documentation
In ECG signal processing, the Removal of 50/60Hz powerline interference from delicate information rich ECG biomedical waveforms is a challenging task! The challenge is further complicated by adjusting for the effects of EMG, such as a patient limb/torso movement or even breathing. A traditional approach adopted by many is to use a 2nd order IIR notch filter:
\(\displaystyle H(z)=\frac{1-2cosw_oz^{-1}+z^{-2}}{1-2rcosw_oz^{-1}+r^2z^{-2}}\)
where, \(w_o=\frac{2\pi f_o}{fs}\) controls the centre frequency, \(f_o\) of the notch, and \(r=1-\frac{\pi BW}{fs}\) controls the bandwidth (-3dB point) of the notch.
What’s the challenge?
As seen above, \(H(z) \) is simple to implement, but the difficulty lies in finding an optimal value of \(r\), as a desirable sharp notch means that the poles are close to unit circle (see right).
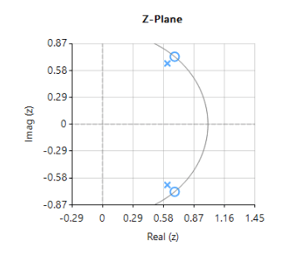
In the presence of stationary interference, e.g. the patient is absolutely still and effects of breathing on the sensor data are minimal this may not be a problem.
However, when considering the effects of EMG on the captured waveform (a much more realistic situation), the IIR filter’s feedback (poles) causes ringing on the filtered waveform, as illustrated below:
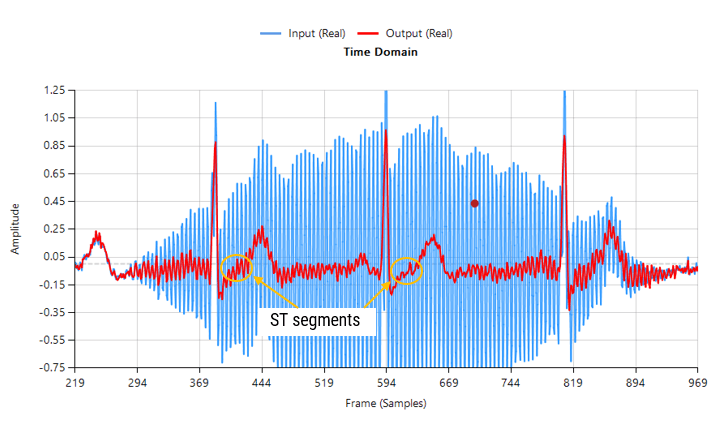
Contaminated ECG with non-stationary 50Hz powerline interference (IIR filtering)
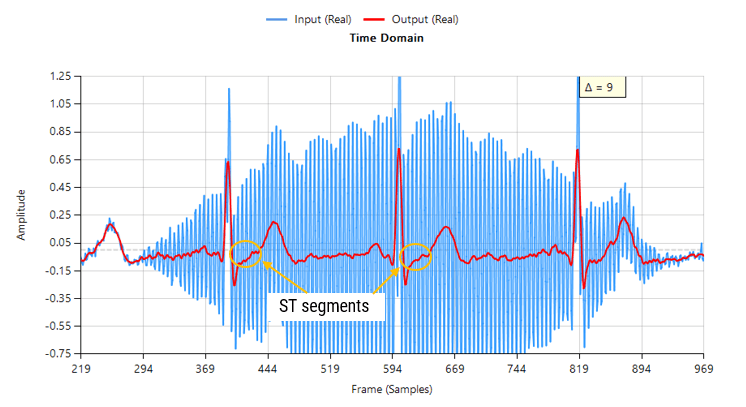
As seen above, although a majority of the 50Hz powerline interference has been removed, there is still significant ringing around the main peaks (filtered output shown in red). This ringing is undesirable for many biomedical applications, as vital cardiac information such as the ST segment cannot be clearly analysed.
The frequency reponse of the IIR used to filter the above ECG data is shown below.
IIR notch filter frequency response
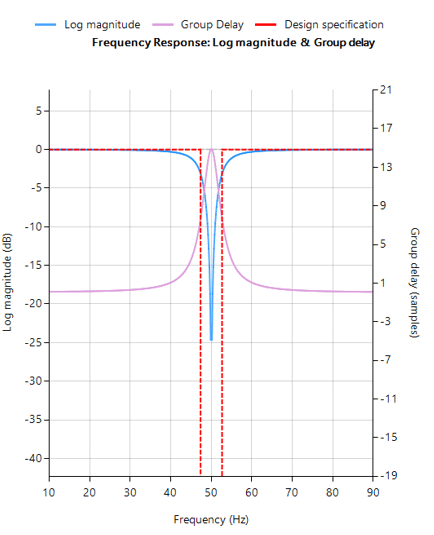
Analysing the plot it can be seen that the filter’s group delay (or average delay) is non-linear but almost zero in the passbands, which means no distortion. The group delay at 50Hz rises to 15 samples, which is the source of the ringing – where the closer to poles are to unit circle the greater the group delay.
ASN FilterScript offers designers the notch() function, which is a direct implemention of H(z), as shown below:
ClearH1; // clear primary filter from cascade
ShowH2DM; // show DM on chart
interface BW={0.1,10,.1,1};
Main()
F=50;
Hd=notch(F,BW,"symbolic");
Num = getnum(Hd); // define numerator coefficients
Den = getden(Hd); // define denominator coefficients
Gain = getgain(Hd); // define gain
Savitzky-Golay FIR filters
A solution to the aforementioned mentioned ringing as well as noise reduction can be achieved by virtue of a Savitzky-Golay lowpass smoothing filter. These filters are FIR filters, and thus have no feedback coefficients and no ringing!
Savitzky-Golay (polynomial) smoothing filters or least-squares smoothing filters are generalizations of the FIR average filter that can better preserve the high-frequency content of the desired signal, at the expense of not removing as much noise as an FIR average. The particular formulation of Savitzky-Golay filters preserves various moment orders better than other smoothing methods, which tend to preserve peak widths and heights better than Savitzky-Golay. As such, Savitzky-Golay filters are very suitable for biomedical data, such as ECG datasets.
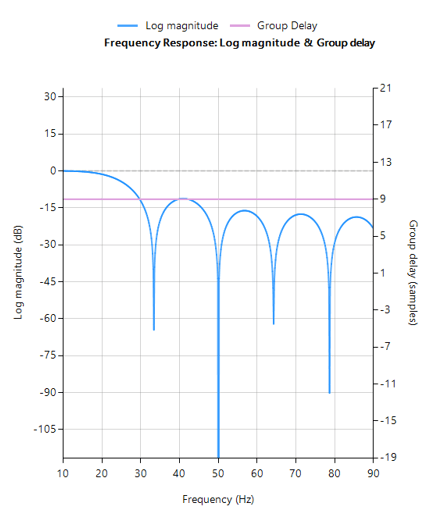
Eliminating the 50Hz powerline component
Designing an 18th order Savitzky-Golay filter with a 4th order polynomial fit (see the example code below), we obtain an FIR filter with a zero distribution as shown on the right. However, as we wish to eliminate the 50Hz component completely, the tool’s P-Z editor can be used to nudge a zero pair (shown in green) to exactly 50Hz.
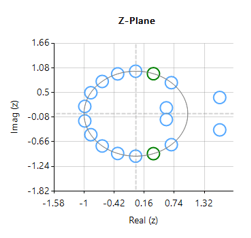
The resulting frequency response is shown below, where it can be seen that there is notch at exactly 50Hz, and the group delay of 9 samples (shown in purple) is constant across the frequency band.
FIR Savitzky-Golay filter frequency response
Passing the tainted ECG dataset through our tweaked Savitzky-Golay filter, and adjusting for the group delay we obtain:
Contaminated ECG with non-stationary 50Hz powerline interference (FIR filtering)
As seen, there are no signs of ringing and the ST segments are now clearly visible for analysis. Notice also how the filter (shown in red) has reduced the measurement noise, emphasising the practicality of Savitzky-Golay filter’s for biomedical signal processing.
A Savitzky-Golay may be designed and optimised in ASN FilterScript via the savgolay() function, as follows:
ClearH1; // clear primary filter from cascade
interface L = {2, 50,2,24};
interface P = {2, 10,1,4};
Main()
Hd=savgolay(L,P,"numeric"); // Design Savitzky-Golay lowpass
Num=getnum(Hd);
Den={1};
Gain=getgain(Hd);
Deployment
This filter may now be deployed to variety of domains via the tool’s automatic code generator, enabling rapid deployment in Matlab, Python and embedded Arm Cortex-M devices.
Author
-

Sanjeev is a RTEI (Real-Time Edge Intelligence) visionary and expert in signals and systems with a track record of successfully developing over 26 commercial products. He is a Distinguished Arm Ambassador and advises top international blue chip companies on their AIoT/RTEI solutions and strategies for I5.0, telemedicine, smart healthcare, smart grids and smart buildings.
View all posts
For many IoT sensor measurement applications, an IIR or FIR filter is just one of the many components needed for an algorithm. This could be a powerline interference canceller for a biomedical application or even a simpler DC loadcell filter. In many cases, it is necessary to integrate a filter into a complete algorithm in another domain. ASN Filter Designer’s automatic code generator greatly simlifies exporting to Python.
Python is a very popular general-purpose programming language with support for numerical computing, allowing for the design of algorithms and performing data analysis. The language’s numpy and signal add-on modules attempt to bridge the gap between numerical algorithmic languages, such as Matlab and more traditional programming languages, such as C/C++. As such, it is much more appealing to experienced programmers, who are used to C/C++ data types, syntax and functionality, rather than Matlab’s scripting language that is more aimed at mathematicans developing algorithmic concepts.
ASN Filter Designer automatic code generator for Python
The ASN Filter Designer greatly simplifies exporting a designed filter to Python via its automatic code generator. The code generator supports all aspects of the ASN Filter Designer, allowing for a complete design comprised of H1, H2 and H3 filters and math operators to be fully integrated with an algorithm in Python.
The Python code generator can be accessed via the filter summary options (as shown on the right). Selecting this option will automatically generate a Python .py design file based on the current design settings.
Version 5 of the tool has a completely revamped filter summary UI, and now includes built in AI to analyse the filter cascade for any potential problems.
The project wizard bundles all of the necessary SDK framework files needed to run the designed filter cascade without the need for any other dependencies or 3rd party plugins.
The framework supports both Real and Complex filters in floating point only, and is built on ASN IP blocks, rather than Python’s signal module, which was seen to struggle with managing complex data. Thus, in order to expedite algorithm development with the framework, the following three demos are provided:
ASNFDPythonDemo: main demo file with various examplesRMSmeterDemo: An RMS amplitude powerline meter demoEMGDataDemo: An EMG biomedical demo with a HPF, 50Hz notch filter and averaging
An example of the summary of all of generated files (including the framework files) is shown below.
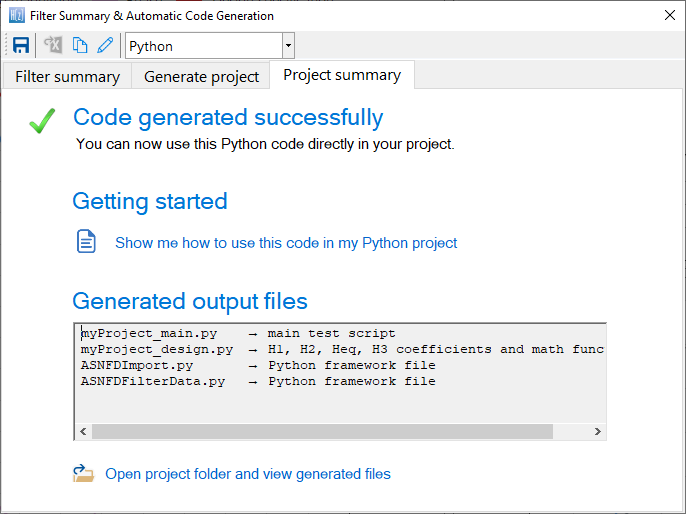
These files can be used directly in your Python project.
For many IoT sensor measurement applications, an IIR or FIR filter is just one of the many components needed for an algorithm. This could be a powerline interference canceller for a biomedical application or even a simpler DC loadcell filter. In many cases, it is necessary to integrate a filter into a complete algorithm in another domain.
Matlab is a well-established numerical computing language developed by the Mathworks that allows for the design of algorithms, matrix data manipulations and data analysis. The product offers a broad range of algorithms and support functions for signal processing applications, and as such is very popular amongst many scientists and engineers worldwide.
ASN Filter Designer automatic code generator for Matlab
The ASN Filter Designer greatly simplifies exporting a designed filter to Matlab via its automatic code generator. The code generator supports all aspects of the ASN Filter Designer, allowing for a complete design comprised of H1, H2 and H3 filters and math operators to be fully integrated with an algorithm in Matlab.
The Matlab code generator can be accessed via the filter summary options (as shown on the right). Selecting this option will automatically generate a Matlab .m file based on the current design.
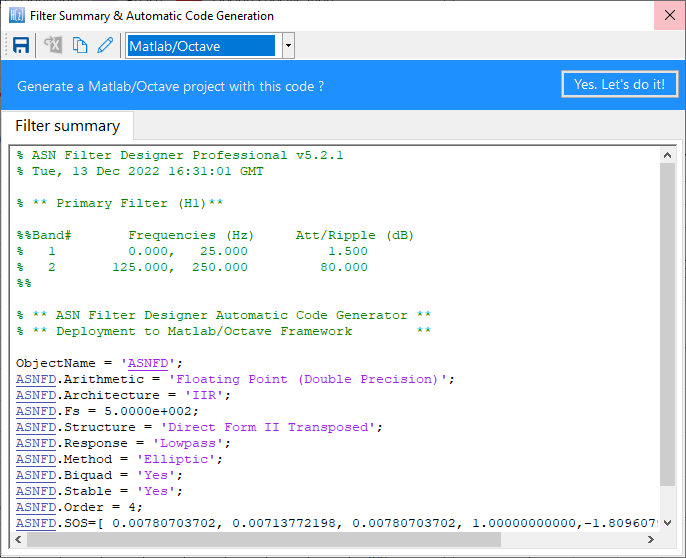
Version 5 of the tool has a completely revamped filter summary UI, and now includes built in AI to analyse the filter cascade for any potential problems. The project wizard bundles all of the necessary SDK framework files needed to run the designed filter cascade without the need for any other dependencies or 3rd party plugins.
Framework files and examples
In order to use the generated code in Matlab without the need for Signal Processing Toolbox, the following three framework files are provided in the ASN Filter Designer’s \Matlab directory:
ASNFDMatlabFilterData.mASNFDMatlabImport.mASNFDFilter.m
These framework files do not have any special Matlab toolbox dependences, and the example script ASNFDMatlabDemo.m demonstrates the simplicity with which the framework can be integrated into your application for your designed filter. Several example filters generated via the automatic code generator are given within ASNFDMatlabDemo.m in order to get you going!
An example of the summary of all of generated files (including the framework files) is shown below.
These files can be used directly in your Matlab/Octave project.
Comparing the results to Matlab’s Signal Processing Toolbox
It’s sometimes informative to compare the results of the ASN Filter Designer’s DSP library functions to that of Matlab’s Signal Processing Toolbox.
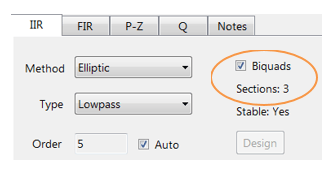
Designing an IIR Chebyshev Type I filter with the following specifications:
| Fs: | 500Hz |
| Passband frequency: | 0-25Hz |
| Type: | Lowpass |
| Method: | Chebyshev Type I |
| Stopband attenuation @ 125Hz: | ≥ 80 dB |
| Passband ripple: | ≤ 0.1dB |
| Order: | 5 |
Graphically entering the specifications into the ASN Filter Designer, and fine tuning the design marker positions, the tool automatically designs the filter as a Biquad cascade. Notice that the tool automatically finds the required filter order, and in essence – automatically produces the filter’s exact technical specification!
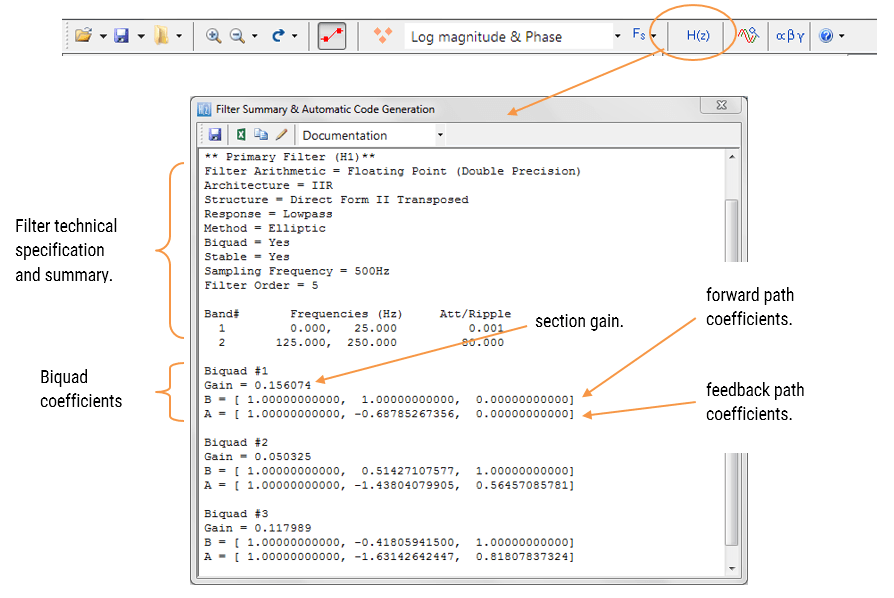
The frequency response of a 5th order IIR Chebyshev Type I lowpass filter meeting the specifications is shown below:
The resulting filter coefficients are:
Designing the same filter in Matlab using Signal Processing Toolbox:
Fs=500; Rp=0.1; Rs=80; F=2*[25,125]/Fs; [N,Wn]=cheb1ord(F(1),F(2),Rp,Rs) [z, p, k] = cheby1(N,Rp,Wn,'low'); % design lowpass [sos,g]=zp2sos(z,p,k,'up') % generate SOS form
Running the script, we get the following, where each row of sos is a biquad arranged as: b0 b1 b2 a0 a1 a2
Analysing both sets of numerator and denominator coefficients, we get exactly the same result! But what about the gain? Matlab outputs a net gain, g = 3.0096e-05 but the ASN Filter Designer optimally assigns a gain to each biquad. Thus, combining the biquad section gains, i.e. 0.078643, 0.013823 and 0.027685 results in a net gain of 3.0096e-05, which is exactly the same net gain as Matlab!
Conclusion: the ASN Filter Designer’s DSP IIR library functions completely match Matlab’s Signal Processing Toolbox results!!
The complete automatically generated code is shown below, where it can be seen that the biquad gains have been pre-multiplied with the feedforward coefficients.
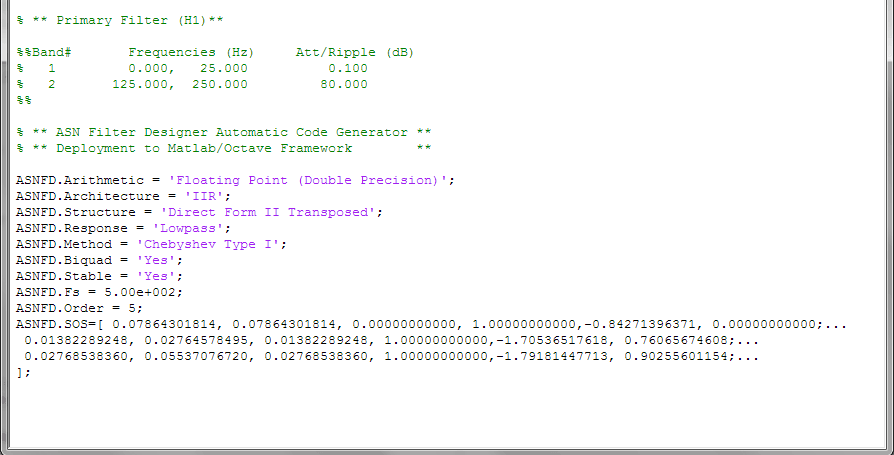
Using the generated code with Signal Processing Toolbox
If you have Signal Processing Toolbox installed, then you may directly use the generated coefficients given in SOS with the sosfilt() command, e.g.
Clear all; ASNFD_SOS=[ 0.07864301814, 0.07864301814, 0.00000000000, 1.00000000000,-0.84271396371, 0.00000000000;... 0.01382289248, 0.02764578495, 0.01382289248, 1.00000000000,-1.70536517618, 0.76065674608;... 0.02768538360, 0.05537076720, 0.02768538360, 1.00000000000,-1.79181447713, 0.90255601154;... ]; y=sosfilt(ASNFD_SOS, x); % x is your input data plot(x,y); % plot results
As seen, it is as simple as copying and pasting the filter coefficients from the ASN Filter Designer’s filter summary into a Matlab script.
Advanced Solutions Nederland B.V.
Lipperkerstraat 146
751DD Enschede
The Netherlands
Tel: +31 652460840
General enquiries: info@advsolned.com
Technical support: support@advsolned.com
Sales enquiries: sales@advsolned.com