Posts

Lineaire fase IIR filters – all-pass equalisatie filters

Hoewel het ontwerp van FIR-filters met lineaire fase een eenvoudige opgave is, geldt dit zeker niet voor IIR-filters die meestal een zeer niet-lineaire faserespons hebben, vooral rond de afsnijfrequenties van het filter. Dit artikel bespreekt waarvoor lineairde eigenschappen die nodig zijn om een digitaal filter een lineaire fase te laten hebben en hoe de passband fase van een IIR filter kan worden aangepast om een lineaire fase te bereiken met behulp van all-pass equalisatie filters.

Waarvoor zijn lineaire fase filters bedoeld?

Digitale filters met lineaire fase hebben het voordeel dat ze alle frequentiecomponenten met dezelfde hoeveelheid vertragen, d.w.z. dat ze de faseverhoudingen van het ingangssignaal behouden. Dit behoud van fase betekent dat het gefilterde signaal de vorm van het oorspronkelijke ingangssignaal behoudt. Deze eigenschap is essentieel voor audiotoepassingen, omdat de signaalvorm van het grootste belang is voor het behoud van de high fidelity in het gefilterde geluid. Nog een ander toepassingsgebied waar dit is vereist, is de ECG biomedische golfvormanalyse, omdat eventuele artefacten die door het filter worden geïntroduceerd, verkeerd kunnen worden geïnterpreteerd als hartafwijkingen.

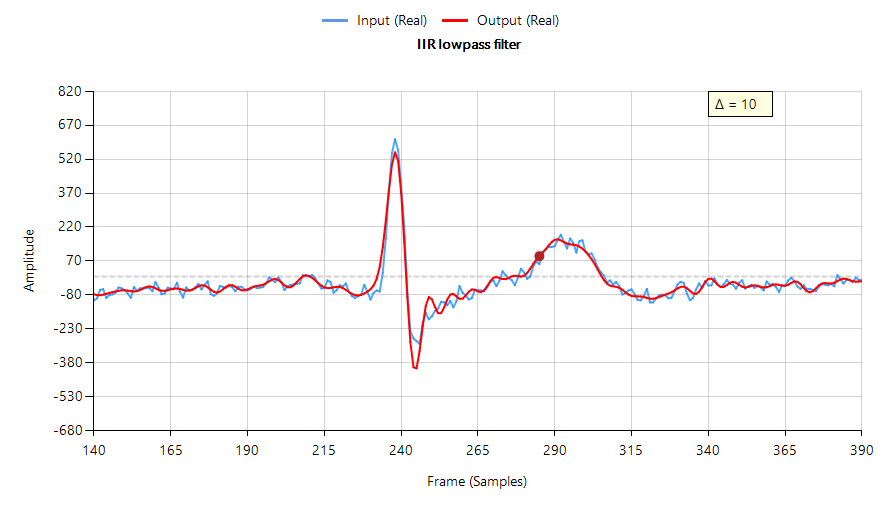
De volgende grafiek toont de filterprestaties van een Chebyshev type I lowpass IIR op ECG-gegevens – invoergolfvorm (weergegeven in blauw) verschoven door 10 samples (\(\small \Delta=10\)) om de groepsvertraging van het filter ongeveer te compenseren. Merk op dat het gefilterde signaal (in rood weergegeven) de oscillaties rond de ECG-piek heeft verzwakt, verbreed en toegevoegd, wat ongewenst is.

Figure 1: IIR lowpass filtering result with phase distortion

Om een digitaal filter een lineaire fase te laten hebben, moet de impulsrespons van een digitaal filter een conjugaat-even of conjugaat-odd-symmetrie hebben rond het midden van het filter. Dit is gemakkelijk te zien voor een FIR-filter,

\(\displaystyle H(z)=\sum\limits_{k=0}^{L-1} b_k z^{-k}\tag{1} \)

Met het volgende constraint op zijn coëfficiënten

\(\displaystyle b_k=\pm\, b^{\ast}_{L-1-k}\tag{2} \)

welke leidt tot

\(\displaystyle z^{L-1}H(z) = \pm\, H^\ast (1/z^\ast)\tag{3} \)

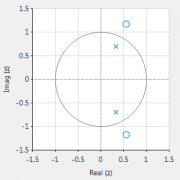
Naar Eqn. 3 kijkend, zien we dat wortels (nullen) van \(\small H(z)\) ook de nullen moeten zijn van  \(\small H^\ast (1/z^\ast)\). Dit betekent dat de wortels van \(\small H(z)\) moet voorkomen in geconjugeerde wederzijdse paren. Bijvoorbeeld wanneer \(\small z_k\) een nul is van \(\small H(z)\), dan moet \(\small H^\ast (1/z^\ast)\) ook een nul zijn.

Waarom hebben IIR filters geen lineaire fase?

Van een digitaal filter wordt gezegd dat het een gebonden ingang, gebonden uitgang stabiel (oftewel: BIBO (Bounded Input, Boundend Output) stabiel), als elke gebonden ingang aanleiding geeft tot een gebonden uitgang. Alle IIR-filters hebben ofwel polen ofwel beide polen en nullen, en moeten BIBO stabiel zijn, d.w.z.

\(\displaystyle \sum_{k=0}^{\infty}\left|h(k)\right|<\infty \tag{4}\)

Hierbij is \(\small h(k)\) de impulsrespons van het filter. Bij het analyseren van Eqn. 4 moet duidelijk zijn dat aan het BIBO-stabiliteitscriterium alleen wordt voldaan als de polen van het systeem binnen de eenheidscirkel liggen, aangezien de eenheidscirkel in het ROC (gebied van convergentie) van het systeem moet worden opgenomen. Het is dus voldoende om te zeggen dat een begrensd ingangssignaal altijd een begrensd uitgangssignaal zal produceren als alle polen binnen de eenheidscirkel liggen.

De nullen daarentegen worden niet beperkt door deze eis en kunnen daardoor overal op het z-vlak liggen, omdat ze niet direct van invloed zijn op de stabiliteit van het systeem. Daarom kan een systeemstabiliteitsanalyse worden uitgevoerd door eerst de wortels van de transferfunctie te berekenen (d.w.z. de wortels van de teller- en noemerpolynomialen) en vervolgens de corresponderende polen en nullen op het z-vlak te plotten.

Door de ontwikkelde logica toe te passen op de polen van een IIR-filter komen we nu tot een zeer belangrijke conclusie waarom IIR-filters geen lineaire fase kunnen hebben..

Een BIBO stabiel filter moet zijn polen binnen de eenheidscirkel hebben, en als zodanig zou een IIR geconjugeerde tegengestelde polen buiten de eenheidscirkel nodig hebben om een lineaire fase te krijgen, waardoor het BIBO onstabiel wordt.

Op basis van deze uitspraak lijkt het niet mogelijk om een IIR te ontwerpen met een lineaire fase. Echter, zoals hieronder besproken, kunnen fase-equalisatiefilters worden gebruikt om de passband-fase respons te lineariseren.

Fase linearisatie met all-pass filters

All-pass fase linearisatiefilters (equalisers) zijn een beproefde methode om de faserespons van een filter te wijzigen zonder de magnitude ervan te beïnvloeden. Een tweede orde (Biquad) all-pass filter wordt gedefinieerd als:

\( A(z)=\Large\frac{r^2-2rcos \left( \frac{2\pi f_c}{fs}\right) z^{-1}+z^{-2}}{1-2rcos \left( \frac{2\pi f_c}{fs}\right)z^{-1}+r^2 z^{-2}}\tag{5} \)

Hierbij is \(\small f_c\) is de centre frequency, \(\small r\) de radius van de polen en \(\small f_s\) de sampling frequency. Merk op hoe de teller- en noemercoëfficiënten als spiegelend aan elkaar zijn gerangschikt. De eigenschap van het spiegelbeeld is wat de all-pass filter zijn gewenste eigenschap geeft, namelijk de ontwerper in staat stellen om de faserespons te veranderen terwijl de magnituderespons constant of vlak blijft over het volledige frequentiespectrum.

Cascadering van een APF (all-pass filter) equalisatie cascade (bestaande uit meerdere APF’s) met een IIR-filter, het basisidee is dat we alleen de fasereactie het passbandgebied moeten lineariseren. De andere gebieden, zoals de overgangsband en de stopband, kunnen worden genegeerd, aangezien eventuele niet-lineairiteiten in deze gebieden van weinig belang zijn voor het totale filterresultaat.

De uitdaging

De APF-cascade klinkt als een ideaal compromis voor deze uitdaging, maar in werkelijkheid is een aanzienlijke hoeveelheid tijd en een zeer zorgvuldige afstemming van de APF-posities nodig om een aanvaardbaar resultaat te bereiken. Elke APF heeft twee variabelen: \(\small f_c\) en \(\small r\) die geoptimaliseerd moeten worden, wat de oplossing bemoeilijkt. Dit wordt verder gecompliceerd door het feit dat hoe meer APF-fasen aan de cascade worden toegevoegd, hoe hoger de totale groepsvertraging (latentie) van het filter wordt. Dit laatste kan problematisch worden voor snelle real-time closed loop controlesystemen die afhankelijk zijn van de lage latency eigenschap van een IIR.

Ondanks deze uitdagingen is de APF-equalizer een goed compromis voor het lineariseren van de kenmerken van een IIR-doorgangsfase.

De APF equaliser

ASN Filter Designer biedt ontwerpers een zeer eenvoudig te gebruiken grafische alle-fase equalizer interface voor het lineariseren van de passband fase van IIR filters. Zoals hieronder te zien is, is de interface zeer intuïtief en stelt het ontwerpers in staat om APF-filters snel te plaatsen en te fine-tunen met de muis. De tool berekent automatisch \(\small f_c\) en \(\small r\), gebaseerd op de markerpositie.

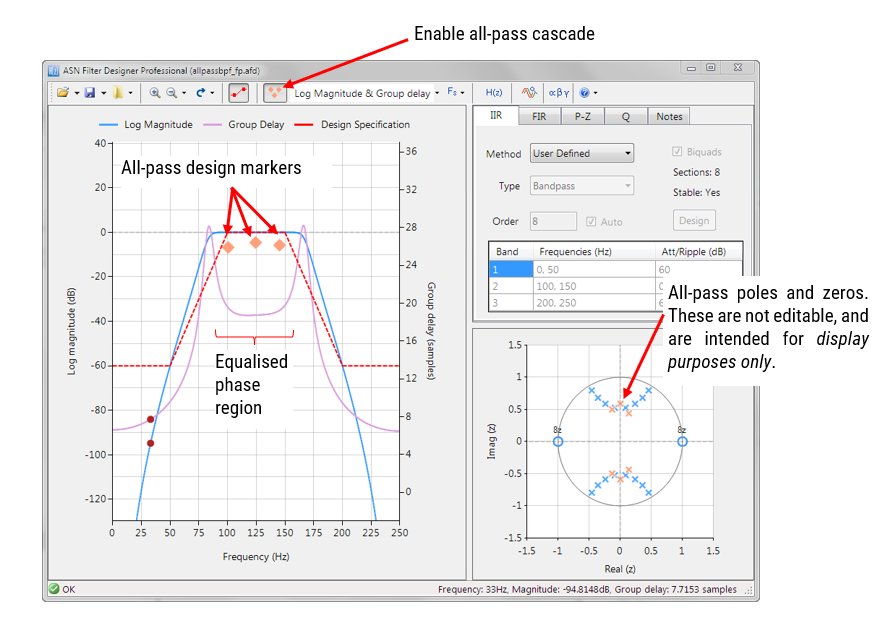
APF equaliser ASN Filter Designer

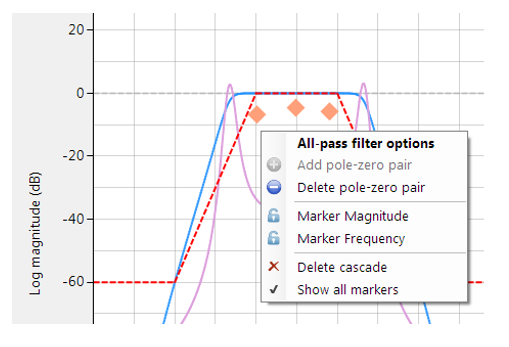
Door met de rechtermuisknop te klikken op de frequentieresponskaart of op een bestaande all-pass design marker wordt een optiemenu weergegeven, zoals links afgebeeld.

U kunt maximaal 10 biquads toevoegen (alleen professionele versie).

Een IIR met lineaire passband fase

Door een equalizer te ontwerpen die bestaat uit drie APF-paren, en deze te cascaderen met het Chebyshev-filter van figuur 1, verkrijgen we een filtergolfvorm die een veel scherpere piek heeft met minder demping en oscillatie dan het oorspronkelijke IIR – zie hieronder. Deze verbetering gaat echter ten koste van drie extra Biquad-filters (de APF-cascade) en een verhoogde groepsvertraging, die nu is opgelopen tot 24 samples ten opzichte van de oorspronkelijke 10 samples.

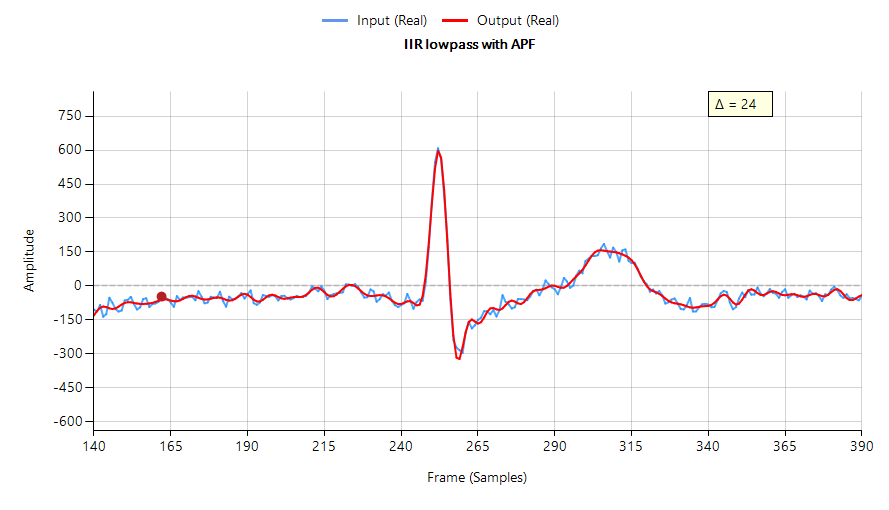
IIR lowpass filtering result with three APF phase equalisation filters (minimal phase distortion)
IIR laagdoorlaatfilterresultaat met drie APF-fase-nivelleringsfilters
(minimale fasevervorming)

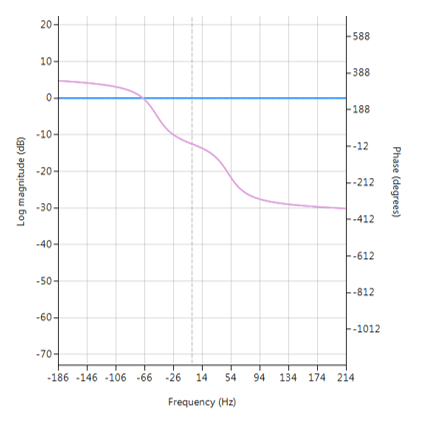
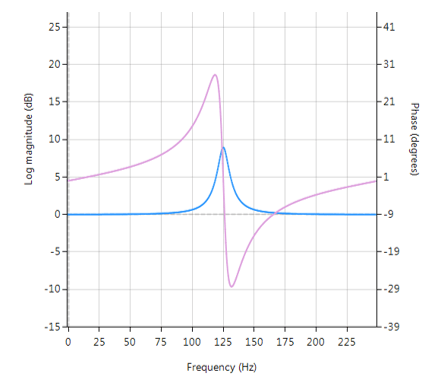
De frequentierespons van zowel het oorspronkelijke IIR als het geequaliseerde IIR worden hieronder weergegeven, waarbij de groepsvertraging (weergegeven in paars) de gemiddelde vertraging van het filter is en een eenvoudiger manier is om de lineariteit te beoordelen.

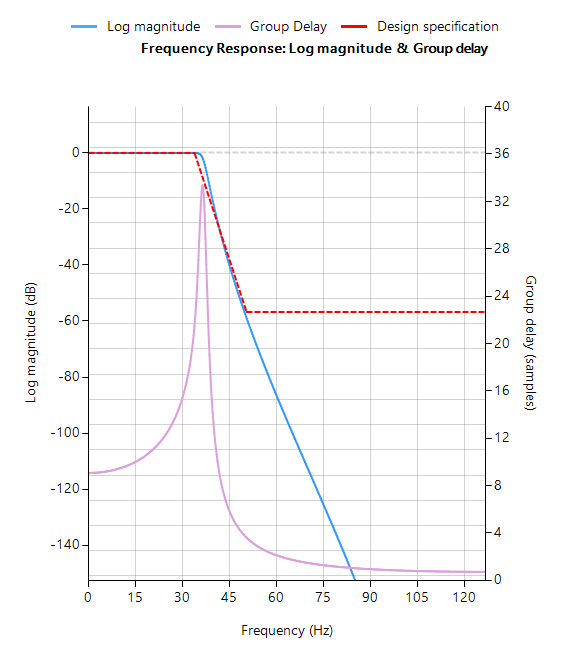
IIR without equalisation cascade
IIR zonder equalisatie cascade

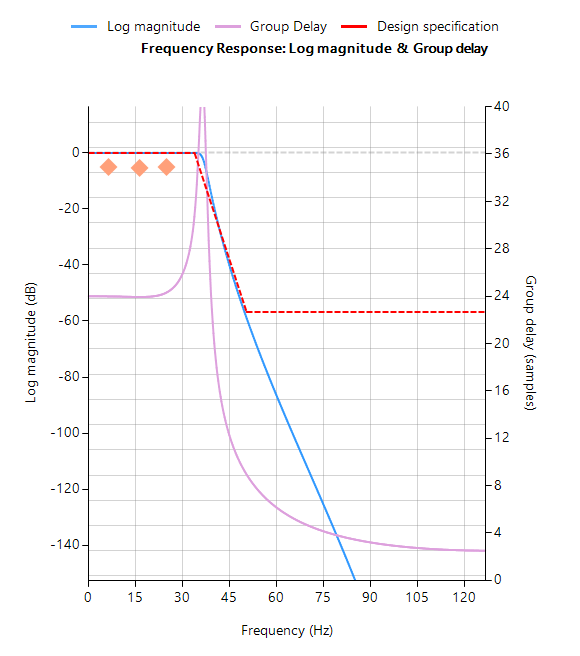
IIR with equalisation cascade
IIR met equalisation cascade

Merk op dat de groepsvertraging van de geëgaliseerde IIR passband (rechts afgebeeld) bijna vlak is, wat bevestigt dat de fase inderdaad lineair is.

Automatische code generatie naar Arm processor cores via CMSIS-DSP

De automatische codegeneratie-engine van de ASN Filter Designer maakt het mogelijk om een ontworpen filter te exporteren naar Cortex-M Arm-gebaseerde processoren via het CMSIS-DSP software raamwerk. De ingebouwde analyse- en helpfuncties van de tool helpen de ontwerper bij het succesvol configureren van het ontwerp voor implementatie.

Voordat de code wordt gegenereerd, moeten de IIR- en equalisatiefilters (d.w.z. H1- en Heq-filters) eerst opnieuw worden geoptimaliseerd (samengevoegd) tot een H1-filter (hoofdfilter) structuur voor implementatie. Het optiemenu is te vinden onder de P-Z tab in de hoofd UI.

Alle ontwerpen van IIR-filters met floating point moeten gebaseerd zijn op Single Precision arithmetic en ofwel een Direct Form I of Direct Form II getransponeerde filterstructuur. De Direct Form II getransponeerde structuur wordt geadviseerd voor floating point implementatie vanwege de hogere numerieke nauwkeurigheid.

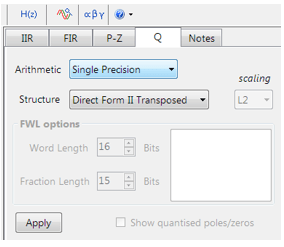
De instellingen voor de kwantiteit en de filterstructuur zijn te vinden onder het tabblad Q (zoals links afgebeeld). Door Arithmetic op Single Precision en Structure op Direct Form II Transposed te zetten en vervolgens op Apply te klikken, wordt de IIR voor het CMSIS-DSP software raamwerk geconficureerd.

Selecteer het Arm CMSIS-DSP raamwerk in het selectievakje in het filteroverzichtsvenster:

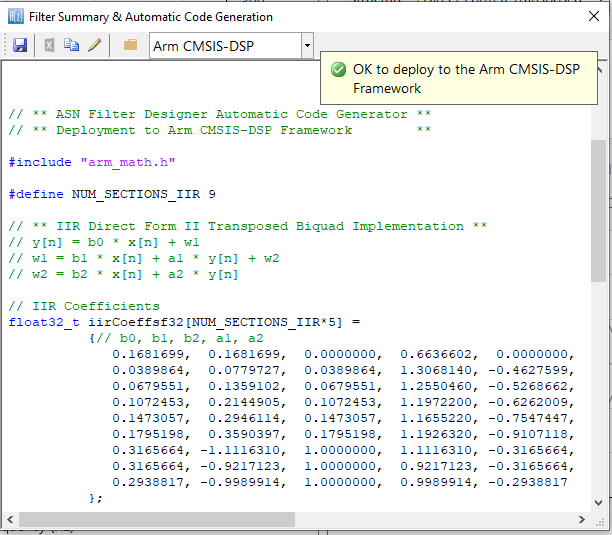
De automatisch gegenereerde C-code op basis van het CMSIS-DSP framework voor directe implementatie op een Arm-gebaseerde Cortex-M processor is hieronder weergegeven:

The ASN Filter Designer's automatic code generator generates all initialisation code, scaling and data structures needed to implement the linearised filter IIR filter via Arm's CMSIS-DSP library.

De automatische codegenerator van de ASN Filter Designer genereert alle initialisatiecode, schaling en datastructuren die nodig zijn om het gelineariseerde filter IIR-filter te implementeren via de CMSIS-DSP-bibliotheek van Arm.

Wat hebben we geleerd?

De wortels van een lineaire fase digitaal filter moeten in geconjugeerde wederzijdse paren voorkomen. Hoewel dit geen probleem is voor een FIR-filter, wordt het voor een IIR-filter onhaalbaar, omdat de polen zowel binnen als buiten de eenheidscirkel zouden moeten liggen, waardoor het filter BIBO onstabiel wordt.

De passband fase-respons van een IIR-filter kan worden gelineariseerd met behulp van een APF-equalisatiecascade. De ASN Filter Designer biedt ontwerpers alles wat ze nodig hebben via een zeer eenvoudig te gebruiken, grafische all-pass fase equalizer interface, om met behulp van de muis een geschikte APF-cascade te ontwerpen!

Het gelineariseerde IIR-filter kan worden geëxporteerd via de automatische codegenerator met behulp van de geoptimaliseerde CMSIS-DSP-bibliotheekfuncties van Arm voor gebruik op elke Cortex-M-microcontroller.

 

 

Download demo

Prijzen en licenties

/0 Comments/by

All-pass filter

All-pass filters

All-pass filters provide a simple way of altering/improving the phase response of an IIR without affecting its magnitude response. As such, they are commonly referred to as phase equalisers and have found particular use in digital audio applications.

In its simplest form, a filter can be constructed from a first order transfer function, i.e.,

\( A(z)=\Large{\frac{r+z^{-1}}{1+r z^{-1}}}  \, \,  \normalsize{; r<1} \)

Analysing \(\small A(z)\), notice that the pole and zero lie on the real z-plane axis and that the pole at radius \(\small r\) has a zero at radius \(\small 1/r\), such that the poles and zeros are reciprocals of another. This property is key to the all-pass filter concept, as we will now see by expanding the concept further to a second order all-pass filter:

\( A(z)=\Large\frac{r^2-2rcos \left( \frac{2\pi f_c}{fs}\right) z^{-1}+z^{-2}}{1-2rcos \left( \frac{2\pi f_c}{fs}\right)z^{-1}+r^2 z^{-2}} \)

Where, \(\small f_c\) is the centre frequency, \(\small r\) is radius of the poles andall pass filter, all-pass filter, allpass filter, all pass pole-zero \(\small f_s\) is the sampling frequency. Notice how the numerator and denominator coefficients are arranged as a mirror image pair of one another.  The mirror image property is what gives the all-pass filter its desirable property, namely allowing the designer to alter the phase response while keeping the magnitude response constant or flat over the complete frequency spectrum.

all pass filter, all-pass filter, allpass, phase equaliser, altering/improving the phase response of an IIR without affecting its magnitude responseFrequency response of all-pass filter:
Notice the constant magnitude spectrum (shown in blue).

Implementation

An All-pass filter may be implemented in ASN FilterScript as follows:
[code language=”java”]
ClearH1; // clear primary filter from cascade

interface radius = {0,2,0.01,0.5}; // radius value
interface fc = {0,fs/2,1,fs/10}; // frequency value

Main()
Num = {radius^2,-2*radius*cos(Twopi*fc/fs),1};
Den = reverse(Num); // mirror image of Num
Gain = 1;

[/code]
For a detailed discussion on IIR filter phase equalisation, and the ASN Filter designer’s APF (all-pass filter) design tool, please refer to the following article.

ASN Filter Designer DSP


Download demo now

Licencing information

Author

  • Dr. Sanjeev Sarpal

    Sanjeev is an AIoT visionary and expert in signals and systems with a track record of successfully developing over 25 commercial products. He is a Distinguished Arm Ambassador and advises top international blue chip companies on their AIoT solutions and strategies for I4.0, telemedicine, smart healthcare, smart grids and smart buildings.

    View all posts

/by

All-pass Peaking/Bell filter

A  Peaking or Bell filter is a type of audio equalisation filter that boosts or attenuates the magnitude of a specified set of frequencies around a centre frequency in order to perform magnitude equalisation. As seen in the plot in the below, the filter gets its name from the shape of the its magnitude spectrum (blue line) which resembles a Bell curve.

Peaking filter or Bell filter, a type of audio equalisation filter that boosts or attenuates the magnitude of a specified set of frequencies around a centre frequency in order to perform magnitude equalisation. As seen in the plot in the below, the filter gets its name from the shape of the its magnitude spectrum (blue line) which resembles a Bell curve.

Frequency response (magnitude shown in blue, phase shown in purple) of a 2nd order Bell filter peaking at 125Hz.

All-pass filters

Central to the Bell filter is the so called All-pass filter. All-pass filters provide a simple way of altering/improving the phase response of an IIR without affecting its magnitude response. As such, they are commonly referred to as phase equalisers and have found particular use in digital audio applications.

A second order all-pass filter is defined as:

\( A(z)=\Large\frac{r^2-2rcos \left( \frac{2\pi f_c}{fs}\right) z^{-1}+z^{-2}}{1-2rcos \left( \frac{2\pi f_c}{fs}\right)z^{-1}+r^2 z^{-2}} \)

Notice how the numerator and denominator coefficients are arranged as a mirror image pair of one another.  The mirror image property is what gives the all-pass filter its desirable property, namely allowing the designer to alter the phase response while keeping the magnitude response constant or flat over the complete frequency spectrum.

A Bell filter can be constructed from the \(A(z)\) filter by the following transfer function:

\(H(z)=\Large\frac{(1+K)+A(z)(1-K)}{2}\)

After some algebraic simplication, we obtain the transfer function for the Peaking or Bell filter as:

\(H(z)=\Large{\frac{1}{2}}\left[\normalsize{(1+K)} + \underbrace{\Large\frac{k_2 + k_1(1+k_2)z^{-1}+z^{-2}}{1+k_1(1+k_2)z^{-1}+k_2 z^{-2}}}_{all-pass filter}\normalsize{(1-K)} \right] \)

  • \(K\) is used to set the gain and sign of the peak
  • \(k_1\) sets the peak centre frequency
  • \(k_2\) sets the bandwidth of the peak

Implementation

A Bell filter may easily be implemented in ASN FilterScript as follows:

ClearH1;  // clear primary filter from cascade
interface BW = {0,2,0.1,0.5}; // filter bandwidth
interface fc = {0, fs/2,fs/100,fs/4}; // peak/notch centre frequency
interface K = {0,3,0.1,0.5}; // gain/sign

Main()

k1=-cos(2*pi*fc/fs);
k2=(1-tan(BW/2))/(1+tan(BW/2));

Pz = {1,k1*(1+k2),k2}; // define denominator coefficients
Qz = {k2,k1*(1+k2),1}; // define numerator coefficients
Num = (Pz*(1+K) + Qz*(1-K))/2;
Den = Pz;
Gain = 1;

This code may now be used to design a suitable Bell filter, where the exact values of \(K, f_c\) and \(BW\) may be easily found by tweaking the interface variables and seeing the results in real-time, as described below.

Designing the filter on the fly

Central to the interactivity of the FilterScript IDE (integrated development environment) are the so called interface variables. An interface variable is simply stated: a scalar input variable that can be used modify a symbolic expression without having to re-compile the code – allowing designers to design on the fly and quickly reach an optimal solution.

As seen in the code example above, interface variables must be defined in the initialisation section of the code, and may contain constants (such as, fs and pi) and simple mathematical operators, such as multiply * and / divide. Where, adding functions to an interface variable is not supported.

An interface variable is defined as vector expression:

interface name = {minimum, maximum, step_size, default_value};

Where, all entries must be real scalars values. Vectors and complex values will not compile.
[arve mp4=”https://www.advsolned.com/wp-content/uploads/2018/07/peakingfilter.mp4″ align=”right” loop=”true” autoplay=”true” nodownload nofullscreen noremoteplayback… /]

Real-time updates

All interface variables are modified via the interface variable controller GUI. After compiling the code, use the interface variable controller to tweak the interface variables values and see the effects on the transfer function. If testing on live audio, you may stream a loaded audio file and adjust the interface variables in real-time in order to hear the effects of the new settings.

ASN Filter Designer Box
Download Demo
Pricing Information
/by