Posts

Exporting IIR/FIR digital filters to C# .NET applications

Over the decades Microsoft has produced various programming languages (e.g. C#, F#, Visual Basic) and flavours of their .NET paradigm, such as the very popular 4.x .NET Framework.  

C# is very popular among Windows developers, as it is based on objected orientated programming concepts together with a few other pearls, such as automatic memory management (something that had to be handled manually in C++), in an attempt to provide many of the advantages of C++ in a much more simplified way.

These pros combined with the .NET Framework’s extensive charting library, UI toolbox, Networking, ML engine libraries and general ease of use in Microsoft Visual Studio was one of the primary reasons that many Windows-based scientific programs (e.g. ASN Filter Designer) were developed using the C# language and .NET Framework.

Over the last few years, Microsoft has tried to consolidate their .NET solution into a single, fast, cross-platform solution with the advent of the .NET Core paradigm. .NET Core is an open-source framework for developing Windows, web applications, services, and mobile applications and it can be run on Windows, Mac and Linux. Microsoft contends that .NET Core is much faster than the .NET Framework since the architecture has been completely rewritten to make it modular, lightweight, fast and cross-platform compatible.

DSP filtering library for C# .NET applications

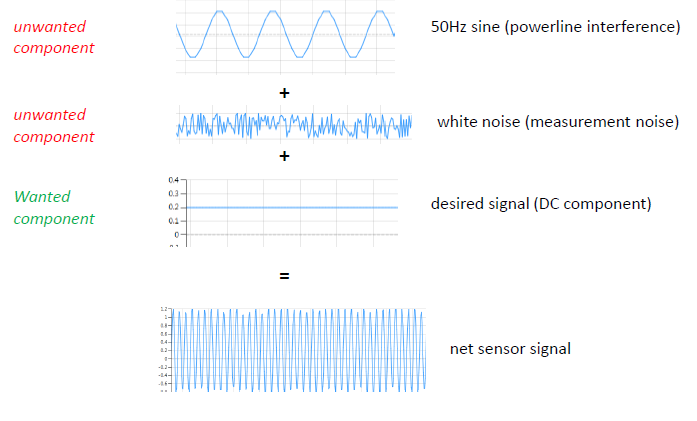
For many modern scientific applications digital filtering of datasets is just one of the many components needed for an algorithm. This could be extracting ECG and PPG biomedical features, cancelling powerline interference or removing the noise from a dataset. In many cases, it is desirable to perform the filtering in real-time on streaming data as part of an algorithm updating dashboard analytics.

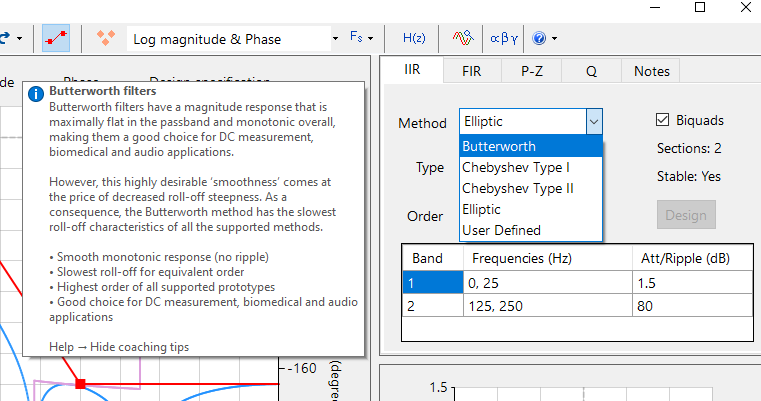
ASN Filter Designer provides .NET developers with an automatic code generator and SDK for developing high-performance data filtering applications in C#.

The tool’s project wizard bundles all of the necessary SDK framework files needed to run a designed filter cascade without the need for any other dependencies or 3rd party plugins. The deployed code is fully compatible with Microsoft Visual Studio and all .NET versions.

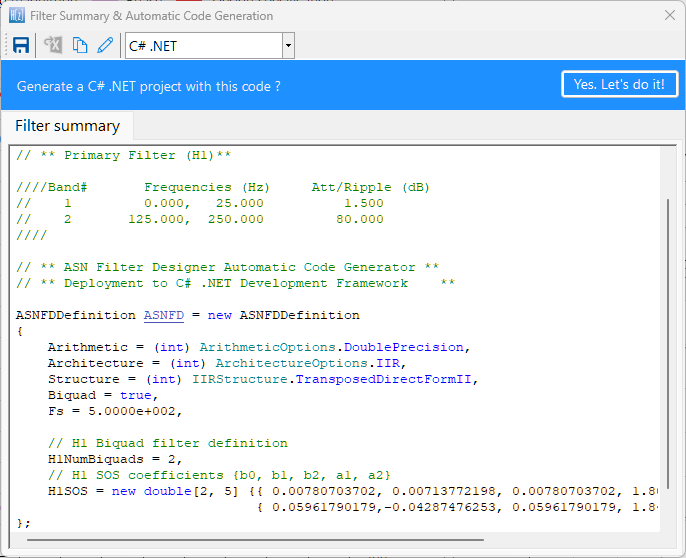
A complete overview of the SDK is available here.

 

 

Download demo now

Licencing information

Author

  • Sanjeev is a RTEI (Real-Time Edge Intelligence) visionary and expert in signals and systems with a track record of successfully developing over 26 commercial products. He is a Distinguished Arm Ambassador and advises top international blue chip companies on their AIoT/RTEI solutions and strategies for I5.0, telemedicine, smart healthcare, smart grids and smart buildings.

    View all posts

/by

FIR notch filter from a lowpass filter

,

Designs an FIR notch filter from a lowpass filter by computing the difference between the prototype lowpass filter and its amplitude complementary

Read more
/0 Comments/by

AIoT optimised DSP filtering library for Arm, RISC-V and MIPS microcontrollers

,

ASN Filter Designer’s new ANSI C SDK framework, provides developers with a comprehensive automatic C code generator for microcontrollers and embedded platforms. This allows developers to directly deploy their AIoT filtering application from within the tool to any STM32, Arduino, ESP32, PIC32, Beagle Bone and other Arm, RISC-V, MIPS microcontrollers for direct use.

Arm’s CMSIS-DSP library vs. ASN’s C SDK Framework

Thanks to our close collaboration with Arm’s architecture team, our new ultra-compact, highly optimised ANSI C based framework provides outstanding performance compared to other commercial DSP libraries, including Arm’s optimised CMSIS-DSP library.

Benchmarks for STM32: M3, M4F and M7F microcontrollers running an 8th order IIR biquad lowpass filter for 1024 samples

As seen, using o1 complier optimisation, our framework is able to surpass Arm’s CMSIS-DSP library’s performance on an M4F and M7F. Although notice that performance of both libraries is worse on the Cortex-M3, as it doesn’t have an FPU. Despite the difference, both libraries perform equally well, but the ASN DSP library has the added advantage of extra functionality and being platform agnostic, making it ideal for variety of biomedical (ECG, EMG, PPG), audio (sound effects, equalisers) , IoT (temperature, gas, pressure) and I4.0 (flow measurement, vibration analysis, CbM) applications.

AIoT applications designed on the newer Cortex-M33F and Cortex-M55F cores can also take advantage of extra filtering blocks, double precision arithmetic support, providing a simple way of implementing high performance AI on the Edge applications within hours.

Advantages for developers

  • A developer can now develop, test and deploy a complete DSP filtering application within the ASN Filter Designer within a few hours. This is very different from a traditional R&D approach that assigns a team of developers for several days in order to achieve the same level of accuracy required for the application.
  • Open source and agnostic code base: In order to allow developers to get the maximum performance for their applications, the ASN-DSP SDK is provided as open source and is written in ANSI C. This means that any embedded processor and any level of compiler optimisation can be used.
  • Memory size required for the ASN-DSP SDK is relativity lower than other standard DSP libraries, which makes the ASN-DSP SDK extremely suitable for microcontrollers that have memory constrains.
  • Using the ASN Filter Designer’s signal analyser tool, developers now can test the performance, accuracy and assess the frequency response of their designed filter and get optimised C code which they can directly use in their application.
  • The SDK also supports some extra filtering functions, such as: a median filter, a moving average filter, all-pass, single section IIR filters, a TKEO biomedical filter, and various non-linear functions, including RMS, Abs, Log and Sqrt.  These functions form the filter cascade within the tool, and can be used to build signal processing applications, such as EMG and ECG biomedical applications.
  • The ASN-DSP SDK supports both single and double precision floating point arithmetic, providing excellent numerical accuracy and wide dynamic range. The library is unique in the sense that it supports double precision arithmetic, which although is not the most optimal for microcontrollers, allows for the implementation of high-fidelity filtering applications.

The ANSI C SDK framework is further extended by our new C# .NET framework, allowing .NET developers to build high performance desktop applications with signal processing capabilities.

Find out more and try it yourself

Benchmarks on a variety of 32-bit embedded platforms, including a biomedical EMG filtering example, are covered in the following application note.

The both framework SDKs are available in ASNFD v5.0, which may be downloaded here.

ASN Filter Designer box
Download Demo
Pricing and Licencing

/0 Comments/by

DSP Audio and Speech Filter Design simplified with ASN Filter Designer

Many Audio/acoustics engineers, researchers and audio hobbyists work with DSP (Digital Signal Processing). In this article, you’ll find out how the ASN Filter Designer helps both experienced audio engineers and engineers where DSP is not their daily job to create digital filters for audio and speech.

For whom?

If you are an audio/acoustics engineer, researcher or even a hobbyist with a little bit of DSP knowledge: ASN Filter Designer is for you! The tool offers the following benefits:

  • Intuitive and easy to use.
  • Logarithmic frequency axis.
  • Save days of time spending calculating on your own for the price of 2-3 hours of work.
  • Few lesser costs then extensive tooling with features you don’t use anyway.
  • Automatic code generation: export for further analysis to Matlab, etc, or to Cortex-M Arm based processors via the Arm CMSIS-DSP software framework.

How DSP for Speech and audio benefit from ASN Filter Designer:

  • Experiment with a variety of equalisation, noise cancellation and sound effect audio filtering algorithms.
  • Perform data analysis in the frequency domain and via specialised methods, including Cepstral analysis on the streaming data.
  • Import your own wav audio files (mono or stereo up to 48kHz) for streaming, and modify the filter characteristics in real-time while listening to the filtered audio stream.

Some features for creating digital filters for Audio and Speech:

Sampling frequency

The sampling frequency may be specified up to 4 decimal places

This is useful for designing filters based on fractional sampling frequencies, such as multiples of the 44.1kHz audio standard. Common examples include audio interpolation filters: 44.1kHz × 128 = 5.6448MHz and 44.1kHz × 256 = 11.2896MHz.

Filter orders of up to 499

Long FIR filters may be constructed, where this is limited to 200 for streaming audio applications.

Logarithmic frequency axis

Perform detailed analysis across the complete audio spectrum 20Hz-20kHz.   

Audio and user data playback streaming

Signal Generator Controller: Choose what you want to listen to; Adjust the amplitude of the input signal
Signal Generator Controller:
Choose what you want to listen to; Adjust the amplitude of the input signal

The signal analyzer allows designers to test their design on audio, real (user) data or synthetic data via the built-in signal generator. Default data playback is implemented as streaming data, providing a simple way of assessing the filter’s dynamic performance, which is especially useful for fixed point implementations. Both frequency domain and time domain charts are fully supported, allowing for design verification via transfer function estimation using the cross and power spectral density functions. As with all other charts, the signal analyzer chart fully supports advanced zooming and panning, as well as comprehensive chart data file export options.

Load .wav for playback

The signal generator allows you to load .wav audio files for playback via the Audio File method. Both mono and stereo formats are fully supported for 8.000, 11.025, 16.000, 22.05, 44.1 and 48kHz. sampling rates. There is no restriction as to the length of the .wav file.

You may add extra signals to input audio stream

Use the signal generator to add sinewaves and white noise to the data stream.

Intuitive data analysis with the mouse

Move the mouse over the chart will automatically produce data markers and data analytics (shown at the bottom right side of the GUI). The signal analyzer is directly coupled to the filter designer GUI. This means that you may modify the filter characteristics, and see the effects in real-time in the signal analyzer. This functionality is very useful when designing audio filters, as the new filter settings can be heard immediately on the streaming audio feed.

Digital filters commonly used in audio and speech

speech and audio engineer researcher working on DSP digital filters microphone headphone

The ASN Filter Designer includes digital filters commonly used in audio such as:

Read review here:

Top marks from Jacob Beningo

/0 Comments/by

DSP vereenvoudigd met ASN Filter Designer

UI experience 2020 pack

Na het downloaden van de ASN Filter Designer willen de meeste mensen gewoon met de tool spelen, om een gevoel te krijgen of het voor hen werkt. Maar hoe ga je aan de slag met de ASN Filter Designer? Op basis van goede gebruikersfeedback wordt ASNFD v4.4 nu geleverd met het UI experience 2020-pakket. Dit pakket bevat gedetailleerde coachingstips, een verbeterde gebruikerservaring en stap-voor-stap instructies om je op weg te helpen met je ontwerp.

Een snel overzicht van de ASN Filter Designer v4.4 vindt je hieronder, een geweldige tool voorDSP IIR/FIR digitaal filterdesign!

De ASN Filter Designer heeft een snelle, intuïtieve gebruikersinterface. Ontwerp interactief, valideer en implementeer jouw uw digitale filter binnen enkele minuten in plaats van uren. Het kan echter moeilijk zijn om een eerste begin te maken met DSP-filterontwerp, vooral wanneer je geen diepgaande kennis hebt van digitale signaalverwerking. De meeste mensen willen gewoon experimenteren met een tool om een gevoel te krijgen of het voor hen werkt (ja, natuurlijk zijn er tutorials en video’s). Maar waar begin je dan?

Start onmiddellijk met experimenteren met het filterontwerp

Daarom hebben we het UI Experience 2020-pakket ontwikkeld. Op basis van de feedback van de gebruikers hebben we gedetailleerde tooltips en animaties van de belangrijkste functionaliteiten gemaakt. Binnen enkele minuten krijgt u een kickstart in functionaliteiten zoals chart zoom, panning en design markers.

This image has an empty alt attribute; its file name is methods_TP-3.png

Coachingstips, verbeterde gebruikerservaring, stap-voor-stap instructies

Gebaseerd op de feedback van de gebruiker bevat het UI Experience 2020-pakket:

  • Uitgebreide coachingtips
  • Gedetailleerde uitleg over ontwerpmethoden en soorten filters
  • Verbeterde gebruikerservaring:
    • cursors
    • animaties
    • visuele effecten
  • Links naar gedetailleerde werkende oplossingen, tutorials en stap-voor-stap instructies
This image has an empty alt attribute; its file name is Coaching-Tip3.png
This image has an empty alt attribute; its file name is Information-FD3.png

De feedback van de gebruikersgemeenschap is zeer positief! Door het verstrekken van gedetailleerde tooltips en animaties van de belangrijkste functionaliteit, is de eerste stap van het ontwerpen van een filter met jouw gewenste specificaties aanzienlijk vereenvoudigd.

Begin dus meteen met de ASN Filterontwerper en bespaar tot 75% op jouw ontwikkelingskosten!

ASN Filter Designer box
ASN Filter Designer box, the powerful DSP Filter Designer platform

Download demo

Prijzen en Licenties
/0 Comments/by

Hoe ASN Filter Designer ingenieurs helpt met digitale filters

DSP voor ingenieurs: de ASN Filter Designer is de ideale tool om de sensordata snel te analyseren en te filteren. Maak een algoritme binnen enkele uren in plaats van dagen. Wanneer u met sensorgegevens werkt, herkent u deze uitdagingen waarschijnlijk:

  • Mijn sensordatasignalen zijn te zwak om zelfs maar een analyse te maken. Daarom heb ik versterking van de signalen nodig
  • Waar ik een vlakke lijn zou verwachten, zien de gegevens eruit als een puinhoop door interferentie en andere vervuiling. Ik moet de gegevens eerst opschonen voordat ik ze analyseer.
Sensor data: wanted components, desired signals (DC components), and unwanted components (50HZ sine powerline interference, white noise). Filter sensor data DSP

Waarschijnlijk heb je tot nu toe dagen of zelfs weken gewerkt aan signaalanalyse en filtering. Het ontwikkelingstraject is over het algemeen langzaam en zeer pijnlijk. Denk maar eens aan het aantal uren dat je had kunnen besparen als je een ontwerptool had gehad die alle algoritmische details voor jou beheerde. ASN Filter Designer is een standaardoplossing voor de industrie die wordt gebruikt door duizenden professionele ontwikkelaars die wereldwijd aan iot-projecten werken.

Onze nauwe samenwerking met Arm en ST zorgt ervoor dat alle ontworpen filters 100% compatibel zijn met alle Arm Cortex-M processoren, zoals de populaire STM32-familie van ST.

Uitdagingen voor ingenieurs

  • 90% van IoT smart sensors zijn gebaseerd op Arm Cortex-M processor technologie
  • Sensor signal processing is moeilijk
  • Sensoren hebben moeite met interferentie en allerlei ongewenste componenten
  • Hoe ontwerp ik een filter dat voldoet aan mijn requirements?
  • Hoe kan ik mijn ontworpen filter controleren op testdata?
  • Voor betere product performance is schone sensor data nodig
  • Tijdrovend proces om een filter op een embedded processor te implementeren
  • Tijd is geld!

Ontwerpers verzanden vaak met traditionele tooling. Deze vereist meestal een iteratieve, trial and error aanpak of deskundige kennis. Met deze aanpak gaat kostbare tijd verloren. ASN Filter Designer helpt u met een interactieve ontwerpmethode. Hierbij voert de tool automatisch de technische specificaties in op basis van eisen die de gebruiker grafisch heeft ingevoerd.

Snelle ontwikkeling van het DSP-algoritme

  • Volledig gevalideerd filterontwerp: geschikt voor toepassing in DSP, Arm microcontroller, FPGA, ASIC of PC-toepassing
  • Automatische gedetailleerde ontwerpdocumentatie: de Filter Designer helpt je met documenatie, waardoor je de peer review kunt versnellen en projectrisico’s verlaagt
  • Eenvoudige overdracht: projectdossier, documentatie en testresultaten bieden een gemakkelijk manier voor overdracht aan collega’s of andere teams
  • Gemakkelijk in te passen in nieuwe scenario’s: het ontwerp kan eenvoudig worden aangepast aan andere eisen en scenario’s, zoals 60Hz interferentieonderdrukking op de voedingslijn, in plaats van de Europese 50Hz.

ASN Filter Designer: de snelle en intuitieve filter designer

De ASN Filter Designer is het ideale hulpmiddel om sensorgegevens snel te analyseren en filteren. Indien nodig kun je jouw gegevens eenvoudig naar tools als Matlab en Python exporteren voor verdere analyse. Daarom is het ideaal voor ingenieurs die een krachtige tool voor signaalanalyse nodig hebben en een datafilter voor hun IOT-toepassing moeten maken. Zeker als je af en toe een datafilter moet maken. Vergeleken met andere tools creeer je een algoritme binnen enkele uren in plaats van dagen.

Exporteer jouw algoritmes naar Matlab, Python of een Arm microcontroller

Je kunt veel tijd besparen doordat je met ASN Filter Designer algoritmes eenvoudig kunt implementeren in Matlab, Python of direct op een Arm-microcontroller omdat de Filter Designer automatisch code generateert.

Onmiddelijke verlichting

Denk eens aan het aantal uren dat je had kunnen besparen als je een ontwerptool had gehad die alle algoritmische details voor je beheerde.

ASN Filter Designer is een standaardoplossing in de sector die wordt gebruikt door duizenden professionele ontwikkelaars die wereldwijd aan ivd-projecten werken. Onze nauwe samenwerking met Arm en ST zorgt ervoor dat alle filters 100% compatibel zijn met alle Arm Cortex-M processoren.

Hoeveel pijnverzachting kun je voor 145 Euro kopen?

Omdat veel technici onze ASN Filterontwerper voor korte tijd nodig hebben, is een licentie van 145 euro voor slechts 3 maanden mogelijk!

Vraag jezelf maar af: is 145 Euro een eerlijke prijs om te betalen voor onmiddellijke pijnverlichting en resultaat? Wij denken van wel. Bovendien hebben we een licentie voor 1 jaar en zelfs een eeuwigdurende licentie. Download de demo om het zelf te zien of neem contact met ons op voor meer informatie

 

 

Download demo

Prijzen en licenties

/0 Comments/by

Chebyshev Filters

Chebyshev I and Chebyshev II filters: what are the advantages and disadvantages? And what is the syntax of Chebyshev, explained with ASN Filterscript

Read more
/0 Comments/by

How to design FIR Filters in ASN Filter Designer

,

What are Finite Impulse Respsonse (FIR) Filters? And how to design FIR Filters in ASN Filter Designer and which filters does ASN Filter Designer support?

Read more
/0 Comments/by

How ASN Filter Designer eases DSP for engineers

,

DSP for engineers: the ASN Filter Designer is the ideal tool to analyze and filter the sensor data quickly. Create an algorithm within hours instead of days. When you are working with sensor data, you probably recognize these challenges:

  • My sensor data signals are too weak to even make an analysis. So, strengthening of the signals is needed
  • Where I would expect a flat line, the data looks like a mess because of interference and other containments. I need to clean the data first before analysis
Sensor data: wanted components, desired signals (DC components), and unwanted components (50HZ sine powerline interference, white noise). Filter sensor data DSP

Until now, you’ve probably spent days or even weeks working on your signal analysis and filtering? The development trajectory is generally slow and very painful.

In fact, just think about the number of hours that you could have saved if you had design tool that managed all of the algorithmic details for you. ASN Filter Designer is an industry standard solution used by thousands of professional developers worldwide working on IoT projects.

Our close collaboration with Arm and ST ensures that all designed filters are 100% compatible with all Arm Cortex-M processors, such as ST’s popular STM32 family.

Challenges for engineers

  • 90% of IoT smart sensors are based on Arm Cortex-M processor technology
  • Sensor signal processing is difficult
  • Sensors have trouble with all kinds of interference and undesirable components
  • How do I design a filter that meets my requirements?
  • How can I verify my designed filter on test data?
  • Clean sensor data is required for better product performance
  • Time consuming process to implement a filter on an embedded processor
  • Time is money!

Designers hit a ‘brick wall’ with traditional tooling. Standard tooling requires an iterative, trial and error approach or expert knowledge. Using this approach, a considerable amount of valuable engineering time is wasted. ASN Filter Designer helps you with an interactive method of design, whereby the tool automatically enters the technical specifications based on the graphical user requirements.

Fast DSP algorithm development

  • Fully validated filter design: suitable for deployment in DSP, micro-controller, FPGA, ASIC or PC application.
  • Automatic detailed design documentation: expediting peer review and lowing project risks by helping the designer create a paper trail.
  • Simple handover: project file, documentation and test results provide a painless route for handover to colleagues or other teams.
  • Easily accommodate other scenarios in the future: Design may be simply modified in the future to accommodate other requirements and scenarios, such as 60Hz powerline interference cancellation, instead of the European 50Hz.

ASN Filter Designer: the fast and intuitive filter designer

The ASN Filter Designer is the ideal tool to analyze and filter the sensor data quickly. When needed, you can easily deploy your data for further analyze for tools such as Matlab and Python. As such it’s ideal for engineers who need and powerful signal analyser and need to create a data filter for their IoT application. Certainly, when you have to create data filtering once in a while. Compared to other tools, you can create an algorithm within hours instead of days.

Easily deploy your algorithms to Matlab, Python, C++ and Arm

A big timesaver of the ASN Filter Designer is that you can easily deploy your algorithms to Matlab, Python, C++ or directly on an Arm microcontroller with the automatic code generators.

Instant pain relief

Just think about the number of hours that you could have saved if you had design tool that managed all of the algorithmic details for you.

ASN Filter Designer is an industry standard solution used by thousands of professional developers worldwide working on IoT projects. Our close collaboration with Arm and ST ensures that the all filters are 100% compatible with all Arm Cortex-M processors.

How much pain relief can 125 Euro buy you?

Because a lot of engineers need our ASN Filter Designer for a short time, a 125 Euro license for just 3 months is possible!

Just ask yourself: is 125 Euro a fair price to pay for instant pain relief and results? We think so. Besides, we have a license for 1 year and even a perpetual license. Download the demo to see for yourself or contact us for more information.

 

 

Download demo now

Licencing information

/0 Comments/by